
信号処理素人老人がScilabの「信号処理のデモ」脱出。「最適化とシミュレーション」のデモに入ってます。前回は「傾斜付きガウス曲線」へのフィッティングでした。今回も非線形フィッティングは続きます。「傾きのある楕円」です。眺めているうちに、彗星だか、小惑星だかの軌道に見えてくるんだこれが。まあ2次元平面デスけど。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
今回「鑑賞」させていただくScilabのデモ
今回は以下のデモ選択画面から起動できるデモ Tilted ellipse(5 params) です。楕円のクセに?パラメータが5個って何よ、と言えばティルト(傾いて)している分で合わせて5個みたいです。
前回同様の、非線形モデルへのデータフィッティングのデモなのですが、前回の加重フィッティングのような技は使っておらず、素直にフィッティングしているみたい。
デモのスクリプトは、以下のファイルです。
ellipse.dem.sce
楕円のパラメータ5個は以下のようです。スクリプト上は、pというベクトルの中に格納されてます。
-
- 楕円の長軸 a、p(1)
- 楕円の短軸 b、p(2)
- 楕円の中心座標 (xc ,yc)、p(3)、p(4)
- 楕円の傾き θ(度)、p(5)
今回も、前回、前々回同様にノイズを含む人工データから元のモデルパラメータを推定してみるというデモです。ただし、前回、前々回は「真値」をキメウチにしてましたが、今回は、真値もランダム生成です。よって、デモを起動する度に表示されるグラフは毎度ことなります。
フィッティングそのものは、毎度お世話になっております datafit関数にお願いしてます。なお、今回独特の後処理として、推定した a、bの値が、正しく長軸、短軸になっているように、検査して逆になっていたら交換するみたいです。知らんけど。
蛇足ですが、cosdとかsindとかいう関数どもをスクリプト内で使役してました。見たこと無い関数じゃん、と思ったら「引数が度」のcosやsinでした。今までラジアン表現のcosやsinの中でπ使って計算していた私は無知でした、トホホ。
シミュレーション結果
デモを実行すると一撃で以下のグラフが求まります。上で述べたように形状は毎回異なります。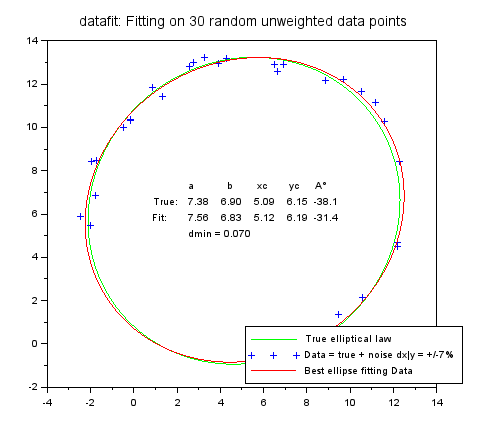
上の楕円は、「惑星」的楕円軌道といいたくなります。以下のケースは長楕円軌道デス。彗星軌道風?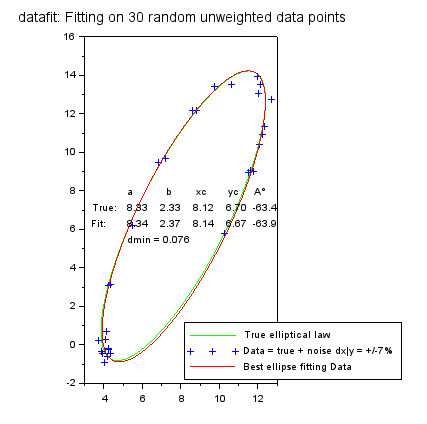
眺めているだけで、妄想が広がるグラフだわいな。