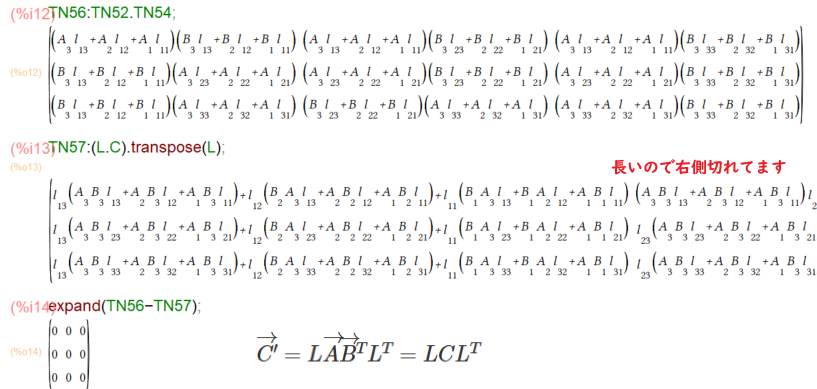溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）を拝読中。前回はベクトル（１階のテンソル）をある直交座標系から別な直交座標系に座標変換する「方法」を練習。今回は余勢を駆って？テンソル（２階）の座標変換を学びます。リハビリ中のお惚け老人にはキツイよ。
※ 「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回「演習ノート」を学ばせていただくのは、「4.2 行列とテンソル」の「4.2.9 直交座標系のベクトル・テンソルの座標変換」の後半、テンソルの座標変換あたりデス。
テンソルの座標変換
前回、ある直交座標系で記述されたベクトルを他の直交座標系に座標変換する方法を学びました。ベクトル（物理量）自体は座標系によらず同じ実体なんだけれども、その成分表示は座標系によって変化するっと。また、ベクトルは１階のテンソルでもあります。
そして今回は２階のテンソルの座標変換です。２階のテンソルの座標変換はベクトルの座標変換則を2回分適用すれば求まることを「演習ノート」は示してくれているみたい。
まずはトートツですが、テンソルCをベクトルAとベクトルBの転置行列の内積で表現するっと。
\(
C =
\overrightarrow {A}
\overrightarrow {B}^T
\)
するとなんやかんやあって、座標変換後のテンソルC’は、前回やったベクトルの座標変換行列Lをつかって以下のように表すことができるっと。
\(
\overrightarrow {C}{}’ =
L \overrightarrow {A} \overrightarrow {B}^T L^T =
L C L^T
\)
以下は「演習ノート」によるなんやかんやの部分。まずは、ベクトルAとベクトルBを持ってきて、ベクトルAとベクトルBの転置行列の内積をとっているところ。これをCとするのだとか。
一方、座標変換行列Lを持ってきて、ベクトルAを座標変換したTN52と、ベクトルBを座標変換したTN53を求めてます。
ところで、
\(
\overrightarrow {B}{}’^T =
\overrightarrow {B}^T L^T
\)
Maxima様に確認してもらうとこんな感じ。左辺＝右辺っす。
そこで肝心要のところを確認するとこんな感じになるみたい。
おお、Lつかって上記のような計算すれば、座標変換後の２階のテンソルC’が求まると。ホントか？
さらに拡張すれば、N階テンソルの成分は、座標変換に対してN個のベクトルの座標変換に対応する変換行列の積によって変換できるらしいっす。まあ、お惚け老人は２階のテンソルで十分お腹いっぱいだけれども。大丈夫か？