拝読中の溝口純敏様著「Maxima を使った物理数学基礎演習ノート」(以下「演習ノート」と略)の今回はグラディエント(勾配、grad)です。遥か半世紀くらい前に学校で習った記憶。まあ、本シリーズでも何度となく練習しているのですが、忘却力の老人はとっくに忘れてます。Maximaではちょいクセ強な処理なので復習回ね。
※ 「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回「演習ノート」を学ばせていただくのは、「4.3 ベクトルの微分」の「4.3.3 勾配(grad)」デス。
過去回での勾配(grad)
何度か練習しています。以下を読むと Mathematica ならお楽で良いなと思う老人です。Maximaではちょいクセ強。
忘却の微分方程式(30) ベクトル解析その1、MathematicaとMaxima
上記過去回では、Mathematicaならキー入力でナブラ演算子(grad)登場し、即座にベクタを与えて計算していけるのでお楽。一方Maximaでは、外部パッケージをload(vect)すると grad関数が使えるようになりますが、呼び出し方がクセ強でした。
-
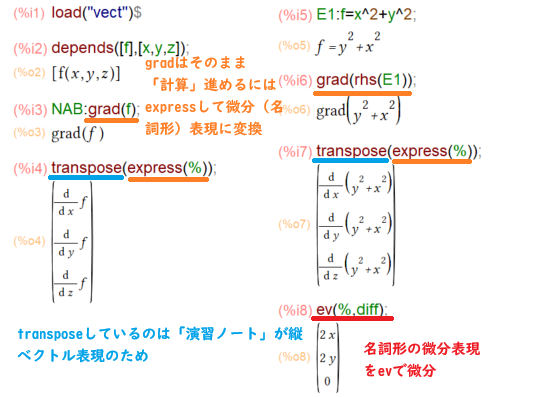
- ただgrad関数に「スカラー場」相当の関数を与えても grad表現のまま
- grad表現を express関数に渡して「微分の名詞形」の表現にまず変換
- それを ev関数で微分(diff)で評価することで計算する
というスタイルです。忘却力の老人は3手順もあると即忘れます。なお、vectパッケージにはdimensionというパラメータもあり、あらかじめ2次元なのか3次元なのか設定しておく必要もあり。
なお、「演習ノート」では縦ベクトル表記を基本としてますが、vectパッケージでは横ベクトル(素のリスト表現)を使っているので、そこの表現の変換にも注意する必要ありです。
忘却の微分方程式(31) ベクトル解析その2、MathematicaとMaxima
上記過去回では、ベクトル場のプロットを行ってます。勿論 gradとった後のベクトル場についても行ってます。
Mathematicaならベクトル場のプロットは2D, 3Dともに一撃、これまたお楽デス。一方、Maximaでは load(plotdf)でさらに追加のパッケージをロードした上でプロットする形になるかと思います。plotdf使うと2Dベクトルは簡単にできましたが、3Dはメンドそう(やってないっす。)
忘却の微分方程式(169) Maxima、{vect}、ベクトル解析パッケージ再び
上記過去回では、vectパッケージの基本的な使い方、先ほどちらっとベクタの次元設定などについても練習してます。また、vectパッケージを導入することで、~記号で外積とれるようになる件についても練習。
忘却の微分方程式(170) Maxima、{vect}、ベクトル解析、gradのプロット
上記はMaximaつかってスカラー関数を3Dプロット(これは簡単にできる)したのち、vectパッケージでgradとって得られたベクトル場を表す関数を plotdfパッケージで2Dベクタプロットする練習です。
演習ノートでのgrad
演習ノートでは vectパッケージをロードして、まずは grad関数そのものを吟味してます。こんな感じ。
演習ノートでは、とくにdimensionの設定なしに、スカラー関数fを3次元設定し、3Dベクタを得る演算子としての grad を導いてます。これは vect パッケージのデフォルトが3次元になっているためです。2次元空間の場合はあらかじめ、dimensionを2に設定しておかないとなりませぬ。
また、vectパッケージが素のリスト表現を「横ベクトル」として扱っているのに対しで、「演習ノート」ではベクトルは「縦ベクトル」表現なので、transpose必須デス。
「演習ノート」ではスカラー関数 f に実体のある関数を与え、gradを適用してみるケースも練習してます。 こんな感じ。
こんな感じ。
expressで微分の名詞形にしておいてから、evで微分評価するところがミソですかな。