
このところずっとターゲットであるバナナ関数(Rosenbrock関数)の最適化デモが続いてます。その中でもネルダーミード法を駆使するfminsearch関数のオプションのいろいろも何度目か。今回はアルゴリズムがの「計算コスト」を可視化するためのオプションです。つべこべ言わずに頑張れ? 違うか?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
fminsearch_optimplotfunccount.sce
前回は、シンプレックスが変形しながら最適値に肉薄していく様子を「表示オプション」一つで知ることができるよ、の回でした。今回はそのときどんだけの計算コストがかかっているのかグラフに描く、の回です。以下のデモ選択画面から起動できます。
今回の「ミソ」は1か所だけ。
opt = optimset ( "PlotFcns" , optimplotfunccount );
長いお名前のオプション、optimplotfunccountデス。これを設定することにより、解にいたるまでのネルダー・ミード法の計算コストがアカラサマになると。ホントか?
デモ実行結果(最適化ー最小値を求めるーの結果)が以下に。ここまでは過去回と同じね。
しかし、上記のoptimplotfunccountの効果は以下のグラフであります。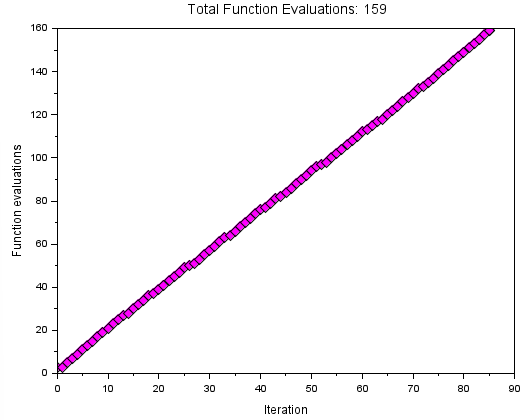
X軸のIterationは、ネルダー・ミード法の反復回数です。 一方、Y軸は目的関数(ここではbanana 関数)を計算した累積関数です。反復回ごとに微妙に出入りはある(シンプレックスの操作に応じて軽いときも重いときもある)ものの、繰り返しとともに目的関数の評価も順調?に増えてますな。まあ、だいたい一本道な感じで良かったケド。他の目的関数は知らず。