
ネルダーミード法を駆使して関数の最適化(値の最小化)を行うfminsearch関数のオプションのデモは続きます。前回は関数評価値が「最適解へ肉薄」していく様子をグラフ化してくれるオプションでした。今回は肉薄しようとしたんだけれど発振しちまったとか、思わぬ方向にヨロケタ、みたいな時にお役立ちのオプションかと。大丈夫か?
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
fminsearch_optimplotx.sce
今回も評価対象の関数はバナナ関数(Rosenbrock関数)デス。果てしなく「評価つづけて」きたので、何も分かっていないお惚け老人にも愛着がわいてきています。
変数空間で最適解(最小値)を見つけるのにfminsearch関数はちょこまかと変数を操作(もうひとつのシンプレックス法ね)しながら最適解へと迫っていきます。まあ、慣れ親しんだバナナ関数の場合、割と素直に解に迫ってくれるみたい。しかし、素性の悪い関数によっては、
-
- ツボにハマって発振始めた
- 初期値の設定悪くて、意図しない方向へ飛んでいってしまった
みたいなこともままありそうです。今回のデモは、アルゴリズムが制御している変数値を「リアルタイム」にグラフ化してくれるオプションのデモです。リアルタイムなので素性が良ければアッという間にグラフは安定しますが、発振したりすると動きつづけるので分かる筈。以下のデモ選択画面から起動できます。
今回も「ミソ」な指定は一か所だけです。
opt = optimset ( "PlotFcns" , optimplotx );
optimplotxオプションね。このオプションつけてバナナ関数を最適化した場合に表示されるグラフ(リアルタイム表示の最後の1枚)が以下に。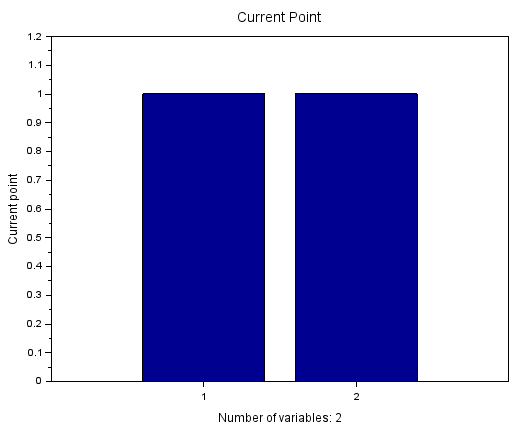
バナナ関数は、変数x1とx2という2次元空間で評価されるので、x軸の変数は2つ。予定どおり、x1=1、x2=1にてバナナ関数の最小値に行き会っているので上のようなグラフがラストとなります。途中はパラパラ動くけれども超早いので、まあユックリ鑑賞することもできんですが。
こういうオプションあったら「万が一」収束しないときとかに使えるかもです。ま、あまりそういう事態になって欲しくはないけど。心がけ次第?ホントか?嘘だよ、多分。