貧乏根性で、折角無料で使えるのだから”Wolfram Mathematica for Raspberry Pi” を使ってみる、ついでに使い方が分かっていないMaxima(PC上)でも同じことをやってみる、の第2回です。前回は入力で、どちらもクセが強いことがすこし分かってきました。今回は分数と小数です。似ているような、似ていないような。
※「忘却の微分方程式」投稿順 index はこちら
Wolfram Mathematicaを学ぶのに使わせていただいておりますのが、以下のチュートリアルです(学生でないのに使わせてもらっていてすいません。)
MathematicaとWolfram言語 数学を学ぶ学生のための入門チュートリアル 分数と小数
Wolfram Mathmaticaで分数入力
早速、分数の入力に入りたいと思いますが、最初から、クセが強い感じがモロ出ました。チュートリアルによると、CTRL+/ で分数の入力になる、ということであったので、1に引き続いてCTRL+/を入力すると分数表示となり、カーソルが分母に移動いたしました。分母に入力できました。が、そのまま+記号を打つと当然ですが、分母に入力されます。慌てて上矢印打てば分子に移動するし、スペースとかタブとかESCとか押してもだめ。次の項を入力するにはどうしたものか?適当にキーを押していて見つけました。右矢印キーを押せばよかったです。
でも無理してCTRL+/で分数形式で入力しなくても / つかって記述しても分数入力は可能でした。見た目を気にしなければ、/の方が入力速いし。そして分数の通分、約分などはTogether[]という関数でできるようです。Togetherしないと、そのままほっとかれるようです。

Maximaで分数入力
Maximaでも CTRL+/ 使えるかと思ってやってみましたが、ダメでした。普通に/で入力します。入力は速くできるし、出力は整形されてくるので、まあいいか。
通分については、やはり関数が異なります。xthru()という名の関数でできました(アイキャッチ画像にxthru関数のExampleを引用させていただきました。)ただ、よくみると分子の順番がMathmaticaとひっくり返っています。数学的には等価ですけど、どうもMaximaの場合、中のアルゴリズムの都合の順序がモロ見えになっている感じがします。なお、何も関数を通さないとそのままほっとかれるのは同じでした。
Wolfram Mathmaticaで小数の出力
浮動小数点数と分数を混在して演算すると出力は浮動小数点数になりました。結果が分数になる計算でも N という関数を通すと浮動小数点数になります。N関数は第2引数として小数点以下の表示桁数を取るようです。
Maximaで小数の出力
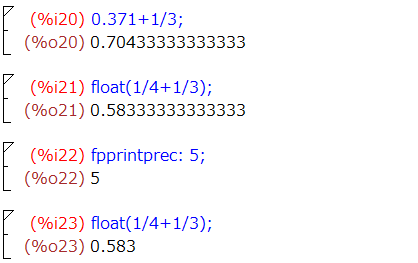
同様に浮動小数点数と分数を混在して演算すると出力は浮動小数点数になりました。分数を浮動小数点数に変換するのはfloat()関数のお役目です。浮動小数点数の表示桁数の制御は、大域変数 fpprintprecというものに値を代入(=ではなくて : 。数学で=は等号だから)しないとなりません。また、ここに立てる値は小数点以下の桁数ではなく、整数部と小数点を含む全桁数みたいです。
Wolfram Mathmaticaで指数表記出力
指数表記(科学表記)は、そのものずばりの ScientificForm[]関数で出力可能でした。100の階乗(100!)など桁数の多い整数は、先ほど出てきた N[] 関数で指数表記にできました。なお、100! とするとそのまま全桁がボロリと出力されます。
Maximaで指数表記出力
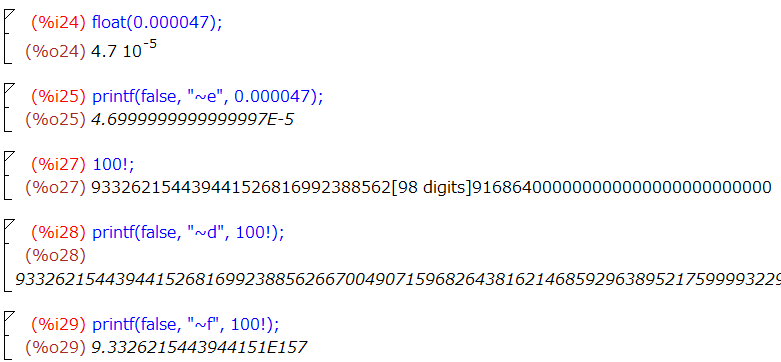
先ほどのfloat()関数に、小数点以下0が多い数値を渡すと勝手に指数表記にしてくれました。しかし、仮数部と指数部の間にはMathematicaで見えたような x 記号などはないです。
そこで、printf()関数に指数表記にするようお願いしてみると指数部に E を使った表記で出力してくれました。こちらの方が間違いないかも。
なお、素で 100! などとすると、途中の数字の桁を端折って「雰囲気」の表示をしてくれます。その代わりprintf()関数に100の階乗の10進表示をお願いすると、全桁を1行にビッシリ表示してくれます(下のキャプチャでは右の方の桁が入りきれずに切れてしまっています。)また、printf()で指数表記にすることも可能でした。
今回は、ほぼ同じことが両方で出来ましたが、どっちもどっちで、クセが強い。