毎回テキトーにグラフを描いてお茶を濁してきたので、今回は多少なりとも統計的な意味に近づきたいです。そこに「飛んで火にいる夏の虫」であったのが今回のシンプルな一元配置の分散分析、one-way ANOVAです。データセットはInsectSprays、「殺虫剤の効果はありや、無しや」と。
※「データのお砂場」投稿順Indexはこちら
R言語に「漏れなくついてくる」であろうサンプルデータセットをABC順に端から舐めてみています。今回問いかけられているのは「6種類の殺虫剤には効果の差がない」(帰無仮説)であります。これを「棄却」し、効果の差がある、と答えられればよろしいのかと(当然、有意水準x%で、という条件つけて。)
データセットの解説ページ
例によってデータセットの解説ページへのリンクは以下です。
Effectiveness of Insect Sprays
農業系の実験場での殺虫剤の種類と虫の数というシンプルなデータです。今回の上記ページには、処理例の手順も記述されているので、分散分析の手順自体はコピペで済ませております(自分でやらないと身につかんよ、自分。)今回の 1元配置の分散分析は、
- 1因子:殺虫剤のタイプ
- 結果:虫の数
です。「他の条件は皆同じ」「実験結果のバラツキは正規分布に従う」という前提のもと、殺虫剤のタイプによって効果が違うのか、それとも違いは単なる偶然の結果、なのかを見抜くというのが処理の意図だと思われます。私が書くのも恐れ多いのですが、
各データの偏差 = 殺虫剤のタイプによる効果(水準間偏差)+同じ殺虫剤での実験回毎のバラツキ(統計誤差)
と分けて考えるのだそうです。真実はバラツキの中にある、のだと。水準間の偏差が、統計誤差に埋もれてしまうようでは効果ありとは言えず。ここでその検証のために登場するのがF分布であるようです。分散分析については立派な方がいろいろ書かれているので、これ以上駄文を書くのは差し控えまする。
生データを見る
例によって生データを見ていきます。データ形式はこれまたシンプルなdata.frameです。実験毎に殺虫剤のタイプ(factor)と虫の数(どんな虫をどうやって数えたなんぞは何も書いてません)が並んでいるだけのものです。まさに1元配置。
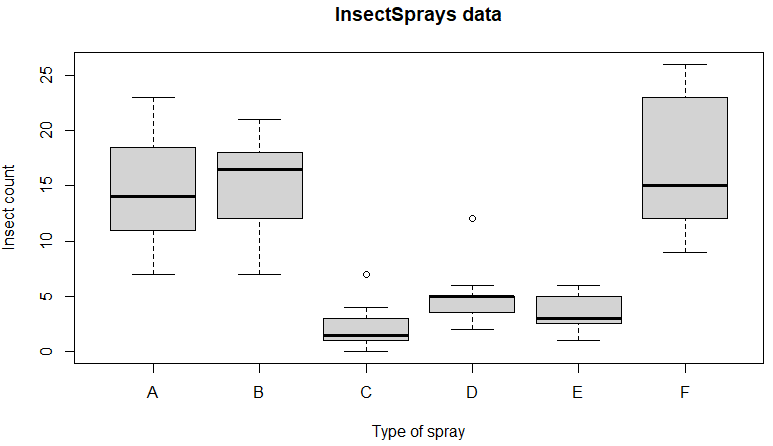
こういうデータを見る時は boxplot (箱ひげ図)にお願いするのが定番のようです。

上記の例題からコピペしたboxplotのコマンドで描かれた箱ひげ図を冒頭のアイキャッチ画像に掲げました。箱ひげ図は、それぞれのFactor(今回は殺虫剤のタイプ)毎に結果の数値のバラツキを描くものです。
- 中央の太い線はメディアン(中央値、平均値じゃないです)
- 箱の上はデータを上から四分割して3/4点
- 箱の下は同じく四分割の1/4点
- 上下に飛び出している棒(ヒゲ)は、箱の上下の幅を基準にある係数をかけて求めていて、今回はデフォルトのままなので係数は1.5だと思います
- 丸ポッチはヒゲからもはみ出した外れ値
これを眺めただけで、「殺虫剤の効果違うじゃん」と私などは思いこんでしまうのであります。でも、ちゃんとANOVAで計算して統計的に確かめよ、ということでしょう。
ANOVA(Analysis of Variance)で計算
例題では、aov()関数で計算結果(リスト構造で複数のデータを含む)を作ってから、それをsummary()関数で「見やすくまとめて」ました。anova()関数というものもあるのですが、結局「見やすくまとめる」ところまで一発でやるだけのようだったです。
計算結果が以下に。
 注目部分は、F Valueと Pr(>F)の値です。特に Pr(>F)です。勝手な理解ですが、この値は「6種類の殺虫剤には効果の差がない」ことを否定できない確率と思って良いみたい。随分小さい値です。一般的な有意水準 5% とか 1% より圧倒的に小さいっす。吹けば飛ぶようなもんですかね。
注目部分は、F Valueと Pr(>F)の値です。特に Pr(>F)です。勝手な理解ですが、この値は「6種類の殺虫剤には効果の差がない」ことを否定できない確率と思って良いみたい。随分小さい値です。一般的な有意水準 5% とか 1% より圧倒的に小さいっす。吹けば飛ぶようなもんですかね。
この値自体はF分布から出てくるものなので、RにF分布のグラフを描いてもらいました。なお自由度は因子数とデータ数から自分で計算することもできますが、上のsummaryのDfというカラムがそうなので、それを見ればよいようです。
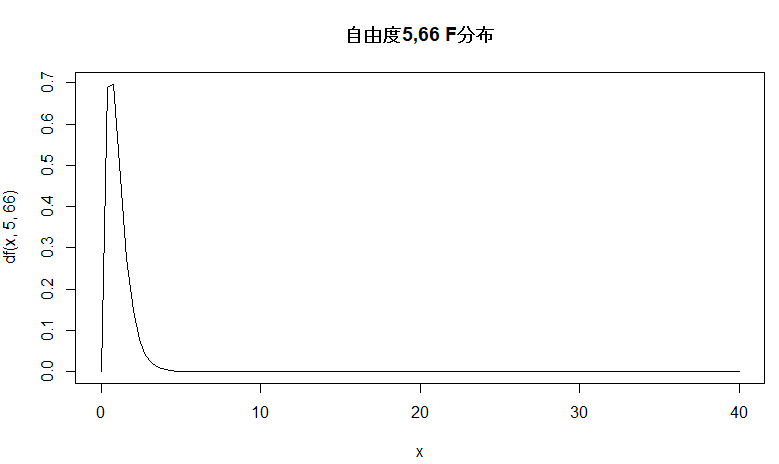 ここにF値34.7というサンプルデータの計算値を当てはめると、ひたすらに0.0に近い値であることが分布からも見てとれます。
ここにF値34.7というサンプルデータの計算値を当てはめると、ひたすらに0.0に近い値であることが分布からも見てとれます。
例題の処理は続く
私としては「帰無仮説を棄却」できたみたいなので、anv()関数の結果だけで大満足なのです。しかし例題の処理は続きます。
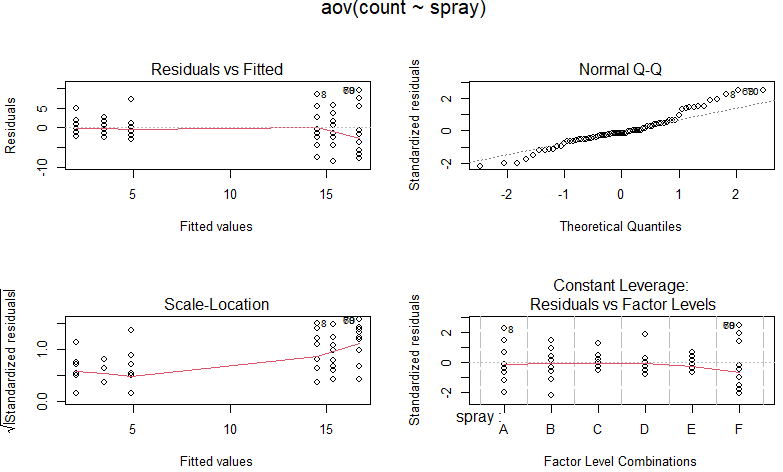
計算した結果のListには、サマリに出力された分析表以外にもいろいろデータ構造が含まれています。「いろいろ吟味」しているみたい。処理コマンドは簡単。Plotするだけ。
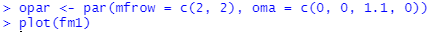
でも出てきたグラフをみてもううむと唸ってしまいます。どう見たらよろしいの?これはそれぞれのデータ構造の意味から勉強しないとダメですな。今日はパスだけれども(手抜き。)
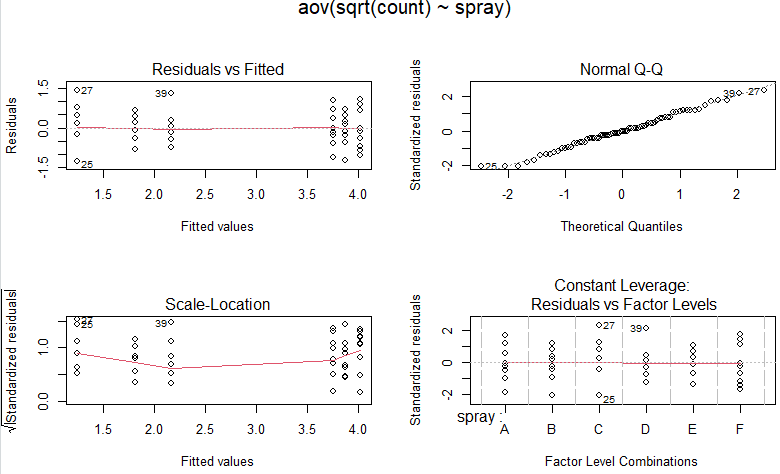
それどころか、虫の数の平方根取ったもので、再度 aov() 処理をかけよ、と。何で平方根?何言っているか意味わかんない。こんな感じ。
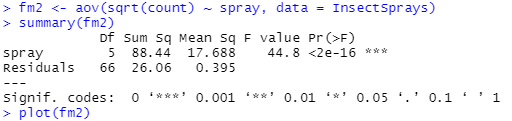
別に平方根かけてもPrの結論は変わらんけど。また良く分からんグラフまで描きます。
平方根でないグラフと平方根の時のグラフをつらつら比べ眺めるに、上よりも下の方が、素直な直線になっているように見えます。単なる見た目の感想です。それがどういう意味を持つのか?そのうち調べないと(何時やるのだ?自分。)