今回はデータを眺めて愕然といたしました。「日本も世界も変わってしまった」のだと。今回のデータセットは1960年代の世界50か国の貯蓄率のデータです。貯蓄率を人口分布や可処分所得から説明する、という仮説を検証するためのものなのです。しかしこの年寄りが驚いたのはその人口の割合です。若いです、日本も世界も。
※「データのお砂場」投稿順Indexはこちら
1960年代の日本と言えば高度成長期であります。この年寄りの朧気な記憶によれば「今の日本に比べたら貧しかったが、皆前向きで、だんだん良くなっている実感」がある時代でした。今回のデータセットはその時代のもの。
さて今回のデータセットの解説ページは以下にあります。
Intercountry Life-Cycle Savings Data
今回の解説ページにはデータセットの処理例も掲載されております。しかし個人的に愕然としたこともあって、処理例の方は通り一遍。グラフを見ながらうだうだしたいと思います。
まずは生データの様子から
生データを見ている様子が以下に。データセットの形式はR特有の data.frameであります。
> data("LifeCycleSavings")
> class(LifeCycleSavings)
[1] "data.frame"
> head(LifeCycleSavings)
sr pop15 pop75 dpi ddpi
Australia 11.43 29.35 2.87 2329.68 2.87
Austria 12.07 23.32 4.41 1507.99 3.93
Belgium 13.17 23.80 4.43 2108.47 3.82
Bolivia 5.75 41.89 1.67 189.13 0.22
Brazil 12.88 42.19 0.83 728.47 4.56
Canada 8.79 31.72 2.85 2982.88 2.43
国ごとに5つの数字(10年間の平均値、景気循環などの変動を取り除くためだと説明あり)が並んでいる表です。項目は以下のとおり
- sr 個人貯蓄総計
- pop15 15歳未満人口割合
- pop75 75歳以上人口割合
- dpi 実質一人当たり可処分所得
- ddpi dpiの成長率
head()で見えている範囲には Japan が無いので1行取り出しました。
Japan 21.10 27.01 1.91 1257.28 8.21
pop15は27.01%、中学生以下の子供が総人口の4分の1以上、そして驚くべきは pop75は1.91%です。後期高齢者が2%に届かなかったのですな。dpiを米国と比べると3分の1以下ですが、伸びは8.21%と凄い。まさに高度成長期。なお成長率のトップは「リビア」でした。石油でも出たのか?
とりあえず、データフレーム全体をplot()関数に食わせてみます。Rはポリモーフィズムの権化なので、適当な実処理に落としてくれるでしょう。
plot(LifeCycleSavings)
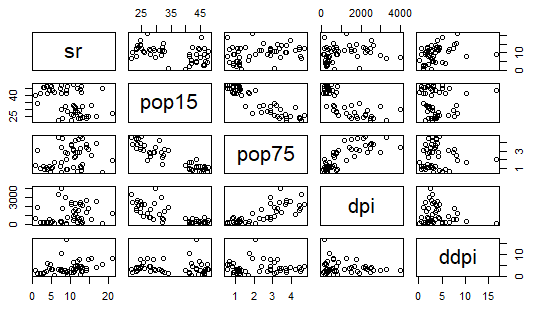
結果はこんな感じ。各列同士の組み合わせ全てについて散布図を描いてくれました。後で、処理例通りに操作しても少しかっこつけたグラフも掲げますが基本は同じ。
個別の散布図を国名付きで描いてみる
もともとのデータセットの目的は多変量の線形回帰と思われるます。その目的からは「国名」はどうでもよいのだと思われますが、今回は個人的に気になります。勝手に以下のような処理をして、国名付きのグラフを描いてみました。ggplot2使用。
pPOP75<-ggplot(data=LifeCycleSavings, aes(pop75, sr, color=rownames(LifeCycleSavings)))+geom_point() pPOP15<-ggplot(data=LifeCycleSavings, aes(pop15, sr, color=rownames(LifeCycleSavings)))+geom_point() pDPI<-ggplot(data=LifeCycleSavings, aes(dpi, sr, color=rownames(LifeCycleSavings)))+geom_point() pDDPI<-ggplot(data=LifeCycleSavings, aes(ddpi, sr, color=rownames(LifeCycleSavings)))+geom_point()
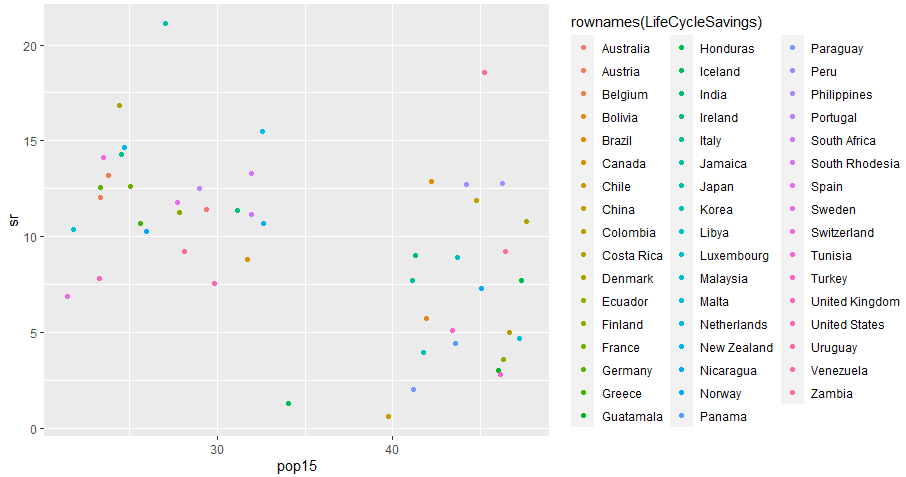
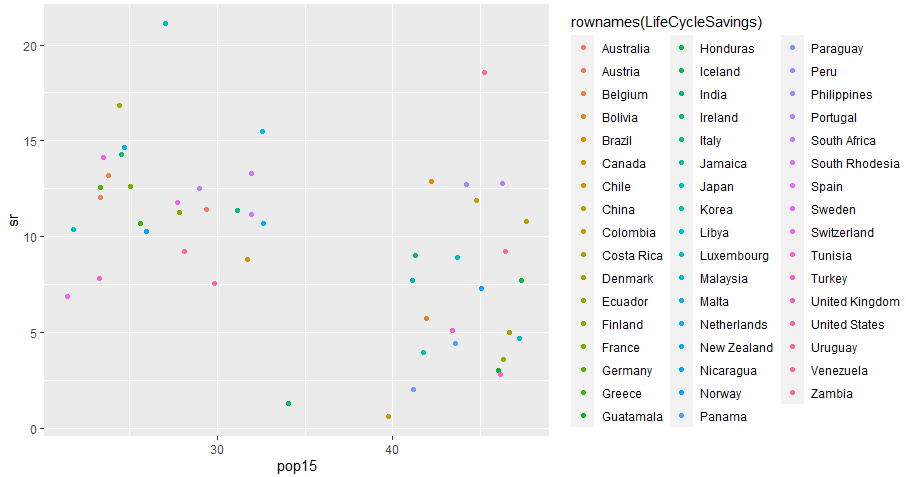
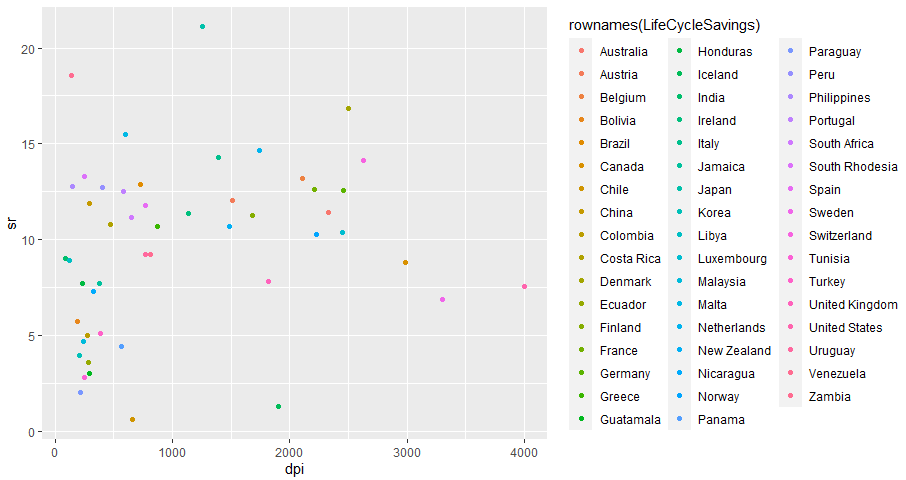
まずは、衝撃のpop15を横軸にとったもの(縦軸は全てsr。)当時の世界が2つに分割されているのを目の当たりにできますな。多分左が先進諸国、右が途上国。中央付近にポッカリと空白領域があり、AIなど使わなくても一撃で分類可能。現在はどうなっているんだろ、混ざっている?
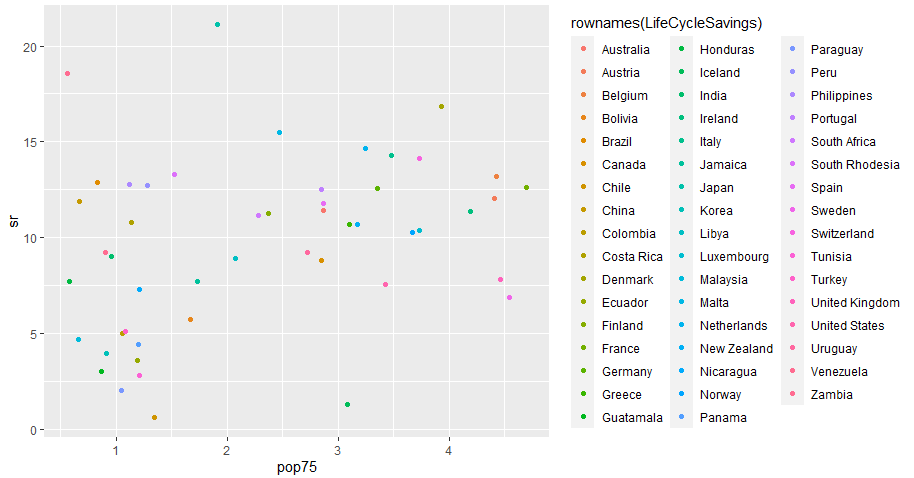
一方、pop75を横軸にとったものが以下に。注目すべきは横軸に記されたパーセンテージ。上限でも5%に達せず。現在データがあったら重ねてみたいですけれども、もしかするとグラフほとんど重ならないかも。。。世界は変わったです。
ついでに横軸を可処分所得にとったもの。
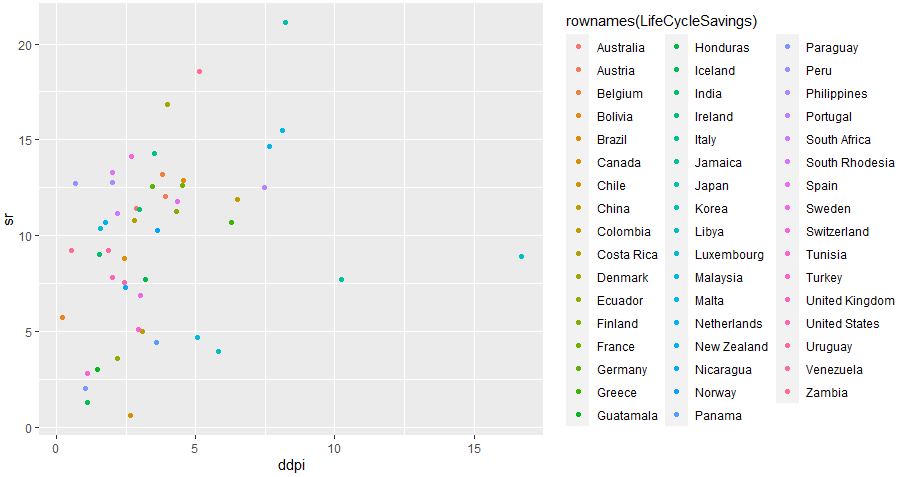
さらについでに横軸を可処分所得の伸び率にしたもの。リビアとジャマイカが1,2フィニッシュ。この時代特有?そして日本は後続グループの中ではトップ。
本来やるべき処理に戻る
先ほどの総当たり散布図は、以下のコマンドで書き換えまする。
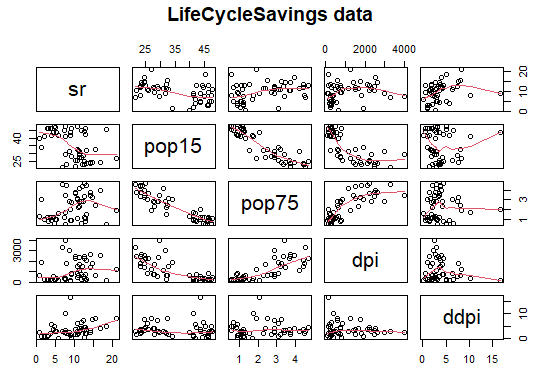
pairs(LifeCycleSavings, panel=panel.smooth, main="LifeCycleSavings data")
するとこんな感じ、赤い線(回帰曲線)が入って、なにやらもっともらしそう。
説明よむと、Franco Modiglianiという先生が貯蓄率は4つの指標で説明できると唱えていたそうなのです。ぶっちゃけRの式でかけば、こういう仮説。
sr ~ pop15 + pop75 + dpi + ddpi
lm()関数使って、線形の重回帰分析せよ、と例題のご指示です。結果は以下に。
> fm1<-lm(sr~pop15+pop75+dpi+ddpi,data=LifeCycleSavings) > summary(fm1) Call: lm(formula = sr ~ pop15 + pop75 + dpi + ddpi, data = LifeCycleSavings) Residuals: Min 1Q Median 3Q Max -8.2422 -2.6857 -0.2488 2.4280 9.7509 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) 28.5660865 7.3545161 3.884 0.000334 *** pop15 -0.4611931 0.1446422 -3.189 0.002603 ** pop75 -1.6914977 1.0835989 -1.561 0.125530 dpi -0.0003369 0.0009311 -0.362 0.719173 ddpi 0.4096949 0.1961971 2.088 0.042471 * --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 Residual standard error: 3.803 on 45 degrees of freedom Multiple R-squared: 0.3385, Adjusted R-squared: 0.2797 F-statistic: 5.756 on 4 and 45 DF, p-value: 0.0007904
本当は仮説に対する結果の当てはまり具合について考察すべきなのでしょうが手が付かず。自分の経験と矛盾しないデータではあるものの、改めて生データを見ると、世界が変わったことにただただ驚くのみ、であります。