今回登場は米国テキサスからフロリダあたりの湿地帯?のようなところに生えている松の一種みたいです。Lobololly pine tree、またの名をテーダマツとな。R言語の「内蔵」サンプル・データセットをABC順に全部「舐めて」みようなどと思いつかなければ多分お目にかかることは無かった植物であります。
テーダマツ、実際どんなものだか見てみたかったので探してみたら、ピッタンコの動画がYouTubeに上がっていました。以下です。
説明を伺いながら、動画で現物を見られるので納得感あり。普通に日本にも生えているくらいの木に見えるのですが、やっぱり米国の松ぼっくりはデカイです。日本のヤツの2~3倍くらいの長さがあるみたい。まあ、シェラ・ネバダ山脈へ行くとパイナップルくらいの大きさの松ぼっくりが落ちていて驚きますが、あそこまでの大きさは無いです。
さて、データセットの解説ページは以下です。
今回は、サンプルデータの処理例も載っているので、最後に処理例通りに処理して「回帰曲線」のグラフを描いてみたいと思います。データセット中のフィールドの意味は以下のようです。
- height 木の高さ[feet]
- age 樹齢[year]
- Seed 木の最大樹高順に紐づけられた種子のソースを示すファクタ?
どうも最後のは「種子の整理番号」的なものみたいです。単なるIDではなく、番号順に何か意味を持たせている。高くなるヤツと低めのヤツで順番ついているらしいもの。
まずは生データ
いつものとおり、まずは生データのロードと観察から。操作は以下の通り
data("Loblolly")
class(Loblolly)
head(Loblolly)
データを見ると、何やら属性情報の付加された data.frame であります。以前学んだとおり、単なる data.frameとみなして処理してしまって良いらしいもの。
まずは生データをグラフにして眺めてみます。ggplot2を利用。グラフを4段階描いてみました。それぞれ g0, g1, g2, g3の中に設定が書き込まれているので、だんだん呼び出してみます。
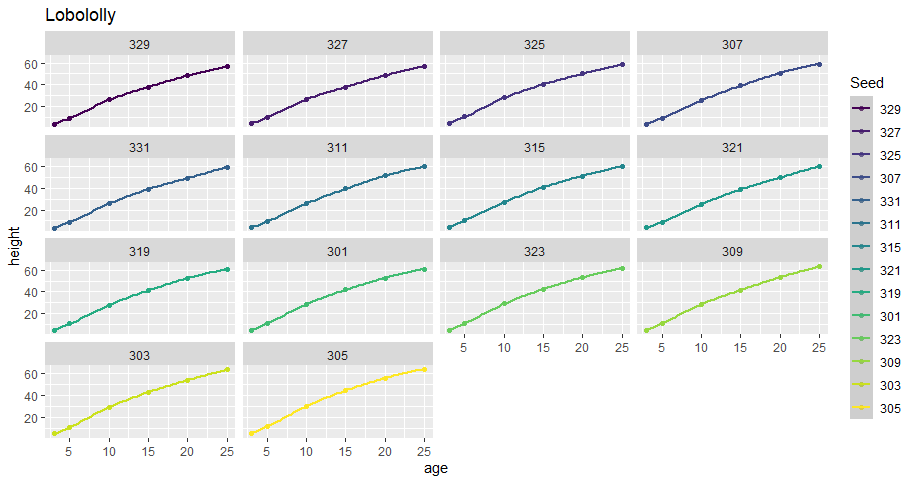
library(ggplot2) g0 <- ggplot(data=Loblolly, aes(age, height, color=Seed))+geom_point() g1 <- g0 + facet_wrap(vars(Seed)) + labs(title="Lobololly") g2 <- g1 + stat_smooth(method="lm") g3 <- g1 + stat_smooth()
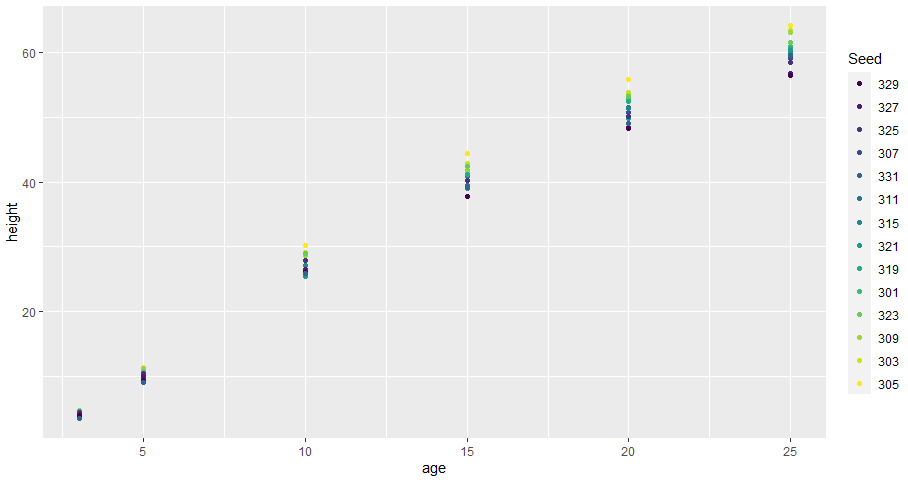
まずは g0、全データを同一面にプロットしたもの。Seedによって色を変えてみました。こんな感じ。なんとなく色が濃ゆいヤツが背が低そうな傾向が見て取れますな。Seed値の順番が効いているものと思われます。
徐々に伸びが落ちている感じ、なんとなくサチりそうな傾向が感じられます。
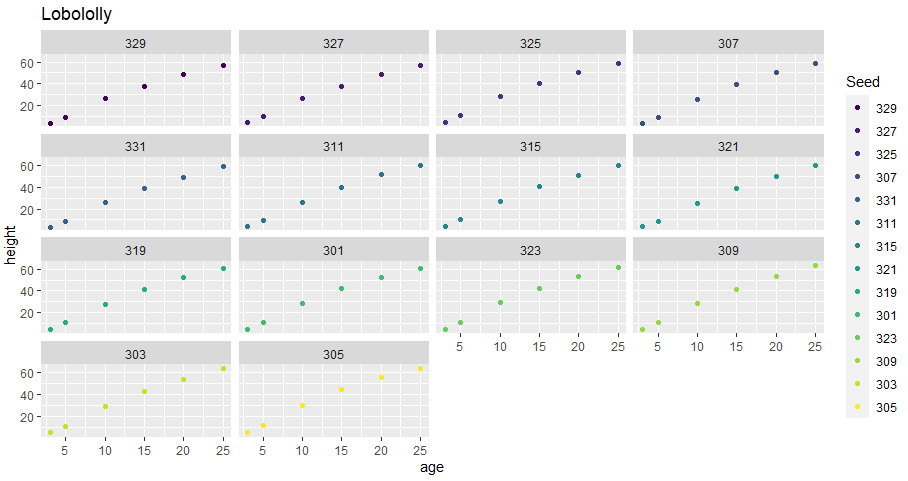
続いてg1、各 Seed毎に facetにしてみました。どれも似たような傾向ではあります。
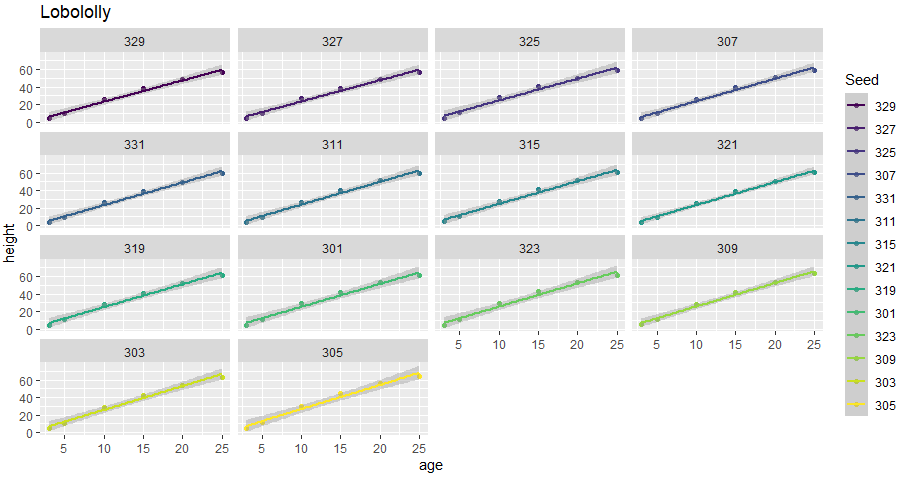
続いてg2、facetに「線形回帰直線」を重ねてみました。この範囲で、このように遠くから見ると、直線でも十分な気もしないでもない。大雑把すぎる?
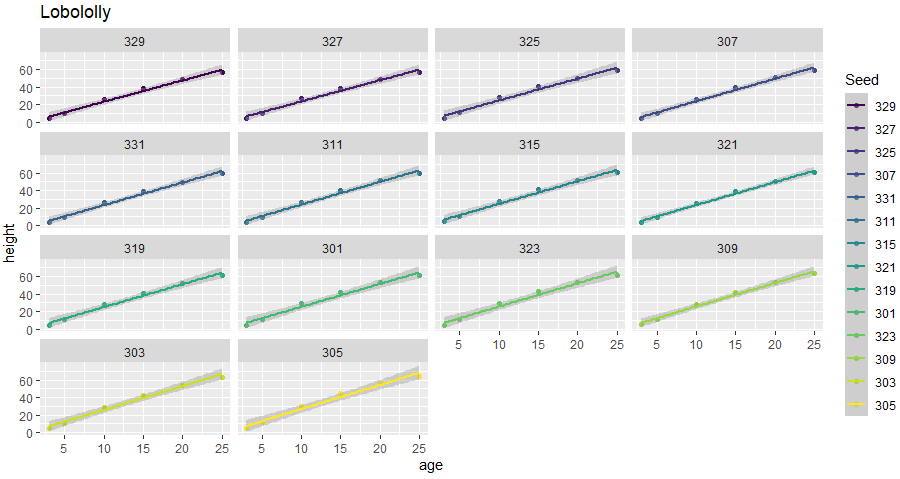
g3は、stat_smooth()「お任せ」で回帰曲線描いてもらいました。あまり意味ないけれど、やはりある高さで頭打ちになりそうな「曲線」が描かれているように見えます。
ただし、最後のg3を描いたら、大量のウォーニングをもらってしまいました。こんな感じ。
「計算結果が NaNになりました」と言われてもな~。NaN(Not A Number)なので、0で割ったとかいうことかい。stat_smooth()のデフォルトがどのような処理をしているのか分からないので追及できまっせん。
処理例通りに回帰曲線を計算してみる
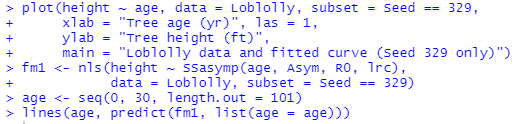
処理例では、タネ番号 329 番に着目して回帰曲線を描いてました。処理の手順は以下の通り。
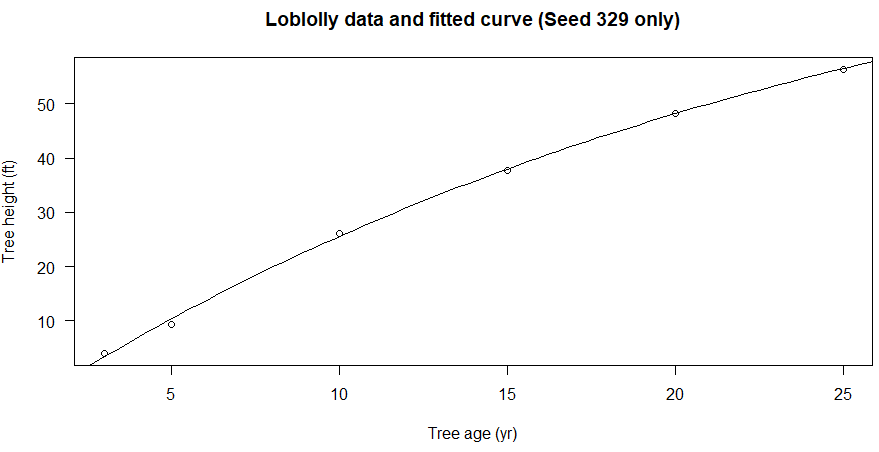
上記のオペレーションで得られるグラフが以下です。普通のplot使っているので素っ気見た目ですが、フィット感?のある回帰曲線じゃないかと。漠然とした感想だな、自分。
例で回帰させているモデルは、以下のものです。
SSasymp
このモデルの式と、グラフの形は以下のページに説明が載っています。
先に上記ページのグラフの形と式を眺めてから、係数を計算した結果のfm1の中身を眺めてみると、ようやく、イメージをつかめます。ホントか?
確かにテーダマツの「成長曲線」は、SSasympモデルでいい感じなのね。