前回の練習、と言って実際に計算しているのはMaxima様ですが、は「ベクトルに垂直な単位ベクトルを求める」でした。今回は「平面と直線の交点の座標を求める」です。霧のかかった朦朧とした頭でもMaxima様にお願いすれば解いてくれる、と。Maxima様は計算間違えなくても入力間違えるなよ、自分。
※「忘却の微分方程式」投稿順 index はこちら
以下の参考書の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。本来は自分の頭で勉強しなければならないのですが、恐れ多い限りであります。年寄りは集中力、気力、記憶力無いのでお許しください。
演習問題2
ネタバレにならぬよう、かいつまんで要約すると以下のような趣旨の問題です。詳しくは上記の御本をご覧になるか、以下のMaximaのコードをお読みくだされ。
平面πと平行で点Aを通る平面αの方程式を求め、続いて直線Lとの交点Bの座標を求めよ
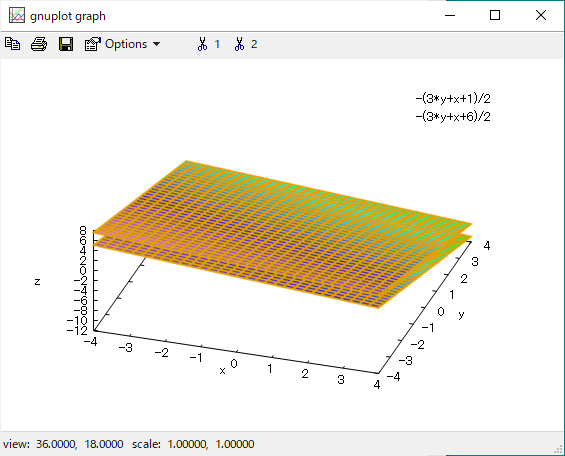
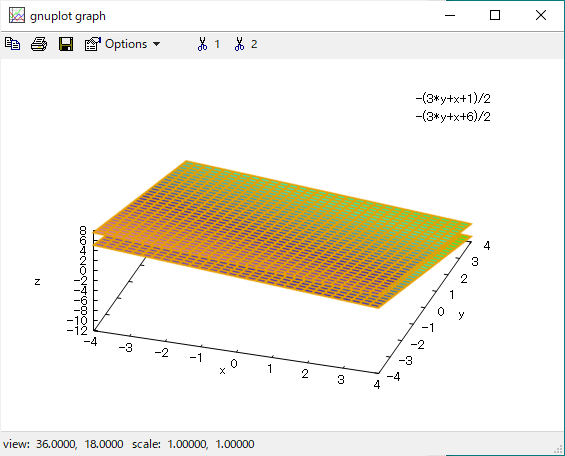
今回は2ステップに分けてスクリプトを書きました。1ステップ目は平面αの方程式を求めるところまでです。ただ方程式をもとめるだけだと、折角のMaximaの威力が無いので、平面αと平面πの3次元プロットも描いてもらいました。
/* 点pA=[ax, ay, az]を通る平面alphaを描く 法線ベクトル vH=[hx, hy, hz] */ pA:[1,-1,-2]$ vH:[1,3,2]$ alpha: vH[1]*(x-pA[1])+vH[2]*(y-pA[2])+vH[3]*(z-pA[3])=0$ alphaGraph: solve(alpha, z)$ pi: vH[1]*x+vH[2]*y+vH[3]*z+1=0$ piGraph: solve(pi, z)$ plot3d([rhs(alphaGraph[1]), rhs(piGraph[1]),[x,-4, 4],[y,-4,4]]);
前回も書きましたが上記のファイルの文字コードはUTF-8でないとバッチ実行したときにエラーになります。
出力された平面の3次元プロットが以下に。
平行な2枚の平面がプロットできたので、まあ、良しですかね。実行には、wxMaximaを使っているので、wxplot3d()関数を使用すれば、上記のグラフは別ウインドウにならずに「埋め込み」できるのです。しかし、ここでは意図的にplot3d()呼んでいます。plot3d()にすると別ウインドウになってしまいますが、視点を変えて色々な方向から様子を観察することができます。
さて肝心の平面αの方程式は変数 alpha に入っている筈なので見てみます。見てみると整理されていない(何もしていないので当然か)ので ratsimp()かけてそれらしい形に整えます。たしかx、y、zの順番も制御できた筈ですが、調べるのがメンドイので今は見送り。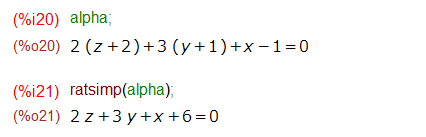
平面αと直線Lの交点Bを求める
前回より、素のリストを、そのままベクトルというか、x, y, zの座標として扱ってます。直線Lの方程式は、演習問題2のヒントにあるように媒介変数で記述してみます。最初、x, y, zの成分毎に3行書いていたのですが、あまりに見苦しいので、map()関数を持ってきて一部のx, y, z要素を1行で書けるようにしてみました。しかし、媒介変数tについて値を求めるところは、「逐次」処理しないとうまく行かなかったので見苦しいままです。どうしたものか。
/* 平面alphaと直線Lの交点Bの座標を求める */ L: [(x-2)/-2=t, y/2=t, (z+1)/1=t]$ W: map(lambda([s,t], solve(s, t)),L,[x,y,z])$ WORKx:subst(rhs(W[1][1]), x, alpha)$ WORKy:subst(rhs(W[2][1]), y, WORKx)$ WORKz:subst(rhs(W[3][1]), z, WORKy)$ Bt: rhs(solve(WORKz, t)[1])$ B: map(lambda([s],subst(Bt, t, rhs(s[1]))),W);
上記を実際にバッチで走らせたところが以下です。途中の処理は $ で出力を抑止し、最後のBの座標出力のところだけ ; で出力しています。こんな感じ。
一応末尾のお答えは合っておると。なお、上記の2番目のスクリプトは、1番目のスクリプトが実行されていないと動きませぬ。
ということで平面と直線の交点は求められる?ホントか?