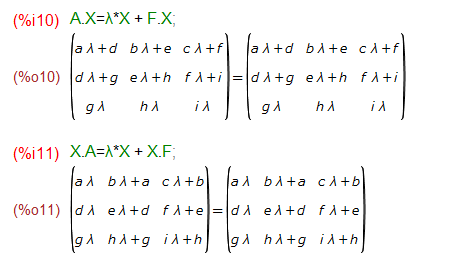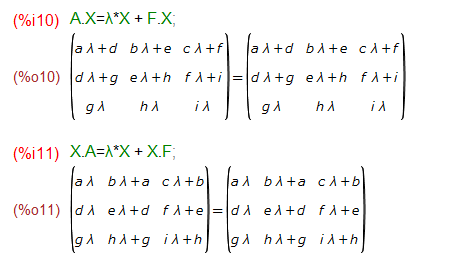今回はようやく線形代数っぽいところに入りました。でも最初は行列の「くせに」スカラー「みたいに」扱えるスカラー行列です。簡単かと思えば、Maximaの操作、クセが強い気がします。個人の感想です。すみません。反復練習していたら身に付くのか?少なくともまだ全然だな、自分。
※「忘却の微分方程式」投稿順 index はこちら
以下の参考書(以下URLは「改訂9」です)の、以前の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。本来目的と違う??
演習問題4の準備的な?
ある条件を満たす3次の正方行列Xを決定する、という問題です。スカラー行列を使って計算を進めていくようです。そこで、問題に入る前に、スカラー行列の生成方法を確かめておきます。
最初のEは単位行列(identity matrix)です。Maximaにはident()関数があるので簡単に生成することができます。
単位行列Eをスカラーλ倍すればスカラー行列が得られます。2番目はスカラー倍している例です。
λEは、対角行列(diagonal matrix)の特殊な例でもあります。Maxima関数 diagmatrixを使って3番目の例のようにしても直接得ることができます。直接生成できるくらいだから「良く使う」ってことみたいですなあ。
さて、求めるべき3x3の正方行列Xを以下の「ベタな方法」で定義しておきます。今のところなんだか分からない、a,b,c…が詰まった行列だと。
ここでスカラー行列の性質を確認したいと思います。
- 行列Xにスカラー行列を左からかけても
- 行列Xにスカラー行列を右からかけても
- 行列Xに単なるスカラーλをかけても
なんだ、結局同じじゃん、と。こんな感じ。
さて、最後に問題に使われる行列Aの定義なのですが、行列Aは、以下の行列Fとスカラー行列を加算したら得られるようになっています。こんな感じ。
さてようやく本題の演習問題です。
問題は以下のとおりです。
AX=XA を満たす3次の正方行列Xを求めよ
既にXは適当なa,b,c…と仮置きしてあるので、上記の性質を満たすような条件を求めるということになります。
AをXに左からかけたときと、右からかけたときでは当然異なる行列が得られる筈ですが、どちらもスカラーλと行列Fと行列Xで書き直せる、と。その様子がこちら。
上の結果から、AとXの関係ではなくFとXの以下の関係が成り立つように決めれば良いことが分かります。
FX=XF
Maxima様に計算をお願いすると以下のようです。行列の要素同士が一致するようにa,b,c…の関係を決めてやると以下のようになりました。あれあれ、Aがいなくなったらλも消えちゃった。
結果は、a, b, c の3つだけからなる上三角行列になるみたい。分かったような分からぬような。
しかし、d:0 とか代入していっても、元の行列Xの中のdは0に勝手に書き換わったりしないのね。それでお答えの行列は上のようにしてみました。いろいろ奥が深いのか、クセが強いのか、Maxima様は。練習はつづく。