昨日の別件投稿にてRISC-VのFPUでのNaN、INF(無限大)、デノーマル数などを再び扱いました。「そういえば」いつも使っているGCCコンパイラでそれらヤバイ奴らはどんな挙動をするんでしょうか?普段、あまり浮動小数点数を使わぬので、実機でやってみることにいたしました。
※ソフトな忘却力 投稿順 index はこちら
実機実験に使用してみたのは、Raspberry Pi 4 model B機(Arm Cortex-A72)です。Raspberry Pi OS<32bit版、Linux>で動作しています。使用した gcc のバージョンは以下のとおりです。
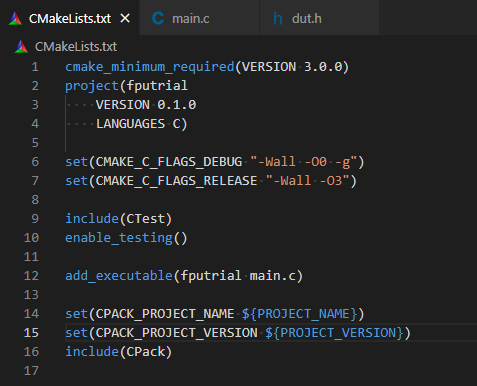
実験は例によってWindows PCからリモート接続しているVScode環境で、Cmakeつかってビルドして行っています。使用したCMakeLists.txtが以下に。DEBUG時とRELEASE時のオプションフラグの設定を明示してあります。特に浮動小数点関係のオプションは付けていない「普通」の設定です。
なお、実験はDEBUGビルドで行いました。
ヤバイ奴らのビットパターン定義
RISC-Vの実験で使ったヘッダファイルを流用してヤバイ奴らのビットパターンを定義してあります。全て単精度浮動小数(float)の値です。
-
- F_M_INF マイナス無限大
- F_M_NORMAL マイナスの正規化数(普通の数)の一例
- F_M_DENORMAL マイナスの非正規化数(FLT_MIN限界以下の数)の一例
- F_M_ZERO マイナスのゼロ
- F_P_ZERO プラスのゼロ
- F_P_DENORMAL プラスの非正規化数の一例
- F_P_NORMAL プラスの正規化数の一例
- F_P_INF プラスの無限大
- F_NAN_SIGNAL SIGNAL型のNaN(Not a Number. 非数)
- F_NAM_QUIET QUIET型のNaN(Not a Number. 非数)
- F_P_NORMAL0 プラスの正規化数でもっとも小さい値(FLT_MIN)
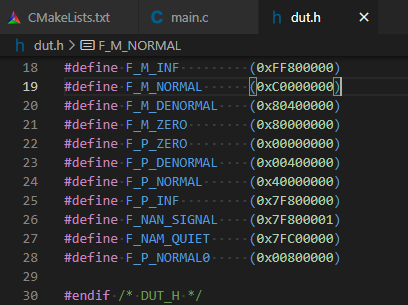
実際のヘッダファイルがこちら。
#ifndef DUT_H
#define DUT_H
#include <stdint.h>
typedef struct {
uint32_t LowW;
uint32_t HighW;
} HighLowW;
typedef union {
uint64_t u64Dat;
HighLowW u32Dat;
double dDat;
float fDat;
} TestFloat;
#define F_M_INF (0xFF800000)
#define F_M_NORMAL (0xC0000000)
#define F_M_DENORMAL (0x80400000)
#define F_M_ZERO (0x80000000)
#define F_P_ZERO (0x00000000)
#define F_P_DENORMAL (0x00400000)
#define F_P_NORMAL (0x40000000)
#define F_P_INF (0x7F800000)
#define F_NAN_SIGNAL (0x7F800001)
#define F_NAM_QUIET (0x7FC00000)
#define F_P_NORMAL0 (0x00800000)
#endif /* DUT_H */
実験に用いたCのコード
以下の疑問点(確認点)をそのままテスト用のコードにしました。
-
- Quiet型のNaNが計算に含まれていたら、結果に伝播するのよね?
- Signal型のNaNを計算に使ったらどうなる?
- ノーマル数をマイナスゼロで割ったら結果はマイナス無限大?
- ノーマル数をプラスゼロで割ったら結果はプラス無限大?
- 無限大を無限大で割ったらどうなる?
- 正規化数を正規化数で割って、非正規化数になる?
#include <stdio.h>
#include <float.h>
#include "dut.h"
void nanQuiet() {
TestFloat f0S, f1S, f2S;
f0S.fDat = 0.0f;
f1S.u32Dat.LowW = F_NAM_QUIET;
f2S.fDat = 0.5f;
f0S.fDat = f2S.fDat * f1S.fDat;
printf("NAN-Quiet\n");
printf(" FLOAT: %e\n", f0S.fDat);
printf(" HEX: %08x\n", f0S.u32Dat.LowW);
}
void nanSignal() {
TestFloat f0S, f1S, f2S;
f0S.fDat = 0.0f;
f1S.u32Dat.LowW = F_NAN_SIGNAL;
f2S.fDat = 0.5f;
f0S.fDat = f2S.fDat * f1S.fDat;
printf("NAN-Signal\n");
printf(" FLOAT: %e\n", f0S.fDat);
printf(" HEX: %08x\n", f0S.u32Dat.LowW);
}
float tryDIVFU(float arg1, uint32_t arg2) {
TestFloat f0S, f1S, f2S;
f0S.fDat = 0.0f;
f1S.u32Dat.LowW = arg2;
f2S.fDat = arg1;
f0S.fDat = f2S.fDat / f1S.fDat;
printf("tryDIVFU %f / %f\n", f2S.fDat, f1S.fDat);
printf(" FLOAT: %e\n", f0S.fDat);
printf(" HEX: %08x\n", f0S.u32Dat.LowW);
return f0S.fDat;
}
float tryDIVUU(uint32_t arg1, uint32_t arg2) {
TestFloat f0S, f1S, f2S;
f0S.fDat = 0.0f;
f1S.u32Dat.LowW = arg2;
f2S.u32Dat.LowW = arg1;
f0S.fDat = f2S.fDat / f1S.fDat;
printf("tryDIVUU %f / %f\n", f2S.fDat, f1S.fDat);
printf(" FLOAT: %e\n", f0S.fDat);
printf(" HEX: %08x\n", f0S.u32Dat.LowW);
return f0S.fDat;
}
float tryDIVUF(uint32_t arg1, float arg2) {
TestFloat f0S, f1S, f2S;
f0S.fDat = 0.0f;
f1S.fDat = arg2;
f2S.u32Dat.LowW = arg1;
f0S.fDat = f2S.fDat / f1S.fDat;
printf("tryDIVUF %e / %f\n", f2S.fDat, f1S.fDat);
printf(" FLOAT: %e\n", f0S.fDat);
printf(" HEX: %08x\n", f0S.u32Dat.LowW);
return f0S.fDat;
}
int main(int argc, char *argv[]) {
printf("FPU trials v0.0\n");
nanQuiet();
nanSignal();
tryDIVFU(0.5, F_P_ZERO);
tryDIVFU(0.5, F_M_ZERO);
tryDIVUU(F_P_INF, F_P_INF);
tryDIVUF(F_P_NORMAL0, 2.0f);
printf("FLT_MIN %e\n",FLT_MIN);
printf("DBL_MIN %e\n",DBL_MIN);
return 0;
}
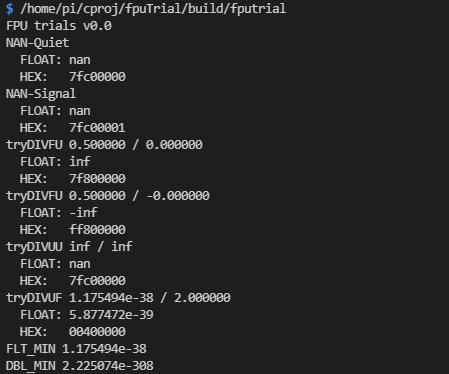
実機上での実験結果
以下は実機上でのデバッグビルドの実行結果です。
結果をまとめると以下のようです。
-
- Quiet型のNaNが計算に含まれていたら、Quiet型のNaNが結果に伝播する。
- Signal型のNaNが計算に含まれていたら、Signal型のNaNが結果に伝播する。なにも設定しない「素の」ままで、gccはSignal型のNaNで例外発生するようになっていないようです。設定方法はあるようですが、要調査。
- ノーマル数をマイナスゼロで割ったら結果はマイナス無限大になる。
- ノーマル数をプラスゼロで割ったら結果はプラス無限大になる。
- 無限大を無限大で割ったら、結果はQuiet型のNaNになった。
- 正規化数を正規化数で割って、非正規化数になることがある。非正規化数か否かはFLT_MINと比較しなければ分からないみたい。
そんなこともあやふやなまま、浮動小数点の計算をするなよ、自分(NaNが出てくるような計算はしないケド。ホントか?)