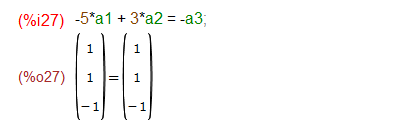前回、係数行列とかrankとかを勉強した後で、今回は線形従属であることを示せとか、線形結合で表せとかいうお題。お楽しみ?の線形空間、部分空間というものに深入り?していくための練習みたいです。Maximaで1問「解ける」ことが分かりさえすれば、何題も練習問題解かなくてもよいじゃん、と。それで反復練習になるのかもし?
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
例題を使わせていただいとりますが、数学の勉強には全然なってないです。すみません。
列ベクトルの生成
キーボードをタイプする手間からするとリストから行ベクトルを入力するのは簡単ですが、列ベクトルにするのはメンドイです。でも数学の場合、縦と横をごっちゃにするなよ、という感じですかね。Eigenとかライブラリ使うと列ベクトル生成関数定義されているみたいですが、とりあえず以下にようにすればOKか?
必要な列ベクトルが定義できたのでお次。
列ベクトルを並べて行列とする
教科書は、続いて「荒業」です。上記の列ベクトル3個を並べて行列にしているのです。maxima上ではどうしたらよいざんしょ。3個並べて[]で括っても、列ベクトル3個のリストになります。行列生成用のmatrix()関数の引数として列ベクトルを与えると、引数はリストでないとダメだと以下のように怒られました。
結局、列を繋げていく addcol() という関数があるのでこれに列ベクトルを与えれば良いのでした。知らないと出来ないよね。
線形従属か否か?
上記3つの列ベクトルが線形従属な関係であるや否やは、直上の行列のrankを求めればよいっと。自分で計算するのはメンドイですが、maxima様にお願いすれば一撃です。こんな感じ。
「2」とな。3-2で自由度が1あるので線形従属である、ようです。
列ベクトルa3をa1とa2の線形結合で表せ、と
3個は線形従属な関係にあるのだから、1個を他の2個で書けるだろうということで、書いてみよ、と。
まずは上で求めた行列Aを階段行列A0に変形してみます。これまた一撃。それに各列ベクトルに乗ずる係数の列ベクトルX0を作り、A0とX0の行列積AXを求めれば、解くべき方程式の入った列ベクトルが現れるという塩梅。
上記の列ベクトルAXの要素を取り出して連立方程式として解けば係数が求まると。行列からの要素の取り出しはちょいとメンドイですが機械的。a3を表せということなので a3 の係数 c3 = 1 としておくと c1, c2, c3が決まります。
a3をa1, a2であらわすためにはa3を移項して符号変えねばなりますまい。式は簡単ですが、一応検算しておくと以下のような感じ。
ううむ、めんどくさがらずにちゃんと a3=5*a1 – 3*a2って書けよ、自分。