ABC順に端からサンプリングデータ、再びカテゴリカルデータの集計登場。UCバークレー校のAdmissions(入試)の学部別、男女別の合否データみたいです。出典は1975年の御本なので、相当古いデータ。しかしこのデータ「シンプソンのパラドックス」を説明するときの定番データらしいです。知らないとモグリ的なやつ?
※「データのお砂場」投稿順Indexはこちら
遥かな古代、といっても1980年代のこと。UCバークレー校に1度だけ見学にいったことがあります。知り合いの知り合いの日本人の方が先生やっておられて、何でか忘れたのですが数名で見学に行かせてもらいました。近くに駐車スペースが無いとかで、確かBartのどこかの駅に車を止めて電車で行きました。既にヒッピーカルチャーの時代は過ぎていたのですが、そこはかとヒッピー的な雰囲気も残っていた気がします。対岸のスタンフォード大の「金持ってるぞ」感からするとやや庶民的な感じでしょうか。どちらもカリフォルニアなので開放的で明るさは共通。
当時のなにか立派な技術を見せていただいた筈ですが失念。覚えているのは壁に先生のランキング表みたいなものが貼られていたこと。バークレーの先生と言えども学生の評価、そして企業から引いてくる献金額にプレッシャー受けてるというお話でした。最近は日本の学校もそうですかね。大学の先生も金を稼がないといかんと。閑話休題。
さて、サンプルデータセットの説明ページは以下にあります。
Student Admissions at UC Berkeley
上記ページを読むと、このデータ「シンプソンのパラドックス」を説明するときの定番みたいです。「シンプソンのパラドックス」について何か良い記事はとぐぐったら、以下の@ITの記事が良さそうでした(個人の感想です。)
シンプソンのパラドックス(Simpson’s paradox)とは?
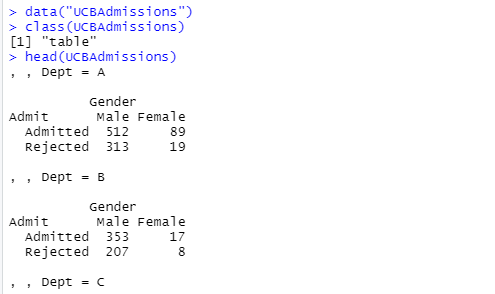
さていつもの生データの確認から
以下のように、3次元の集計テーブルです。集計は、
- 学部(名前はA,B,Cと特定できないようになっている)
- 性別
- 合格者、不合格者数
まずは自力で
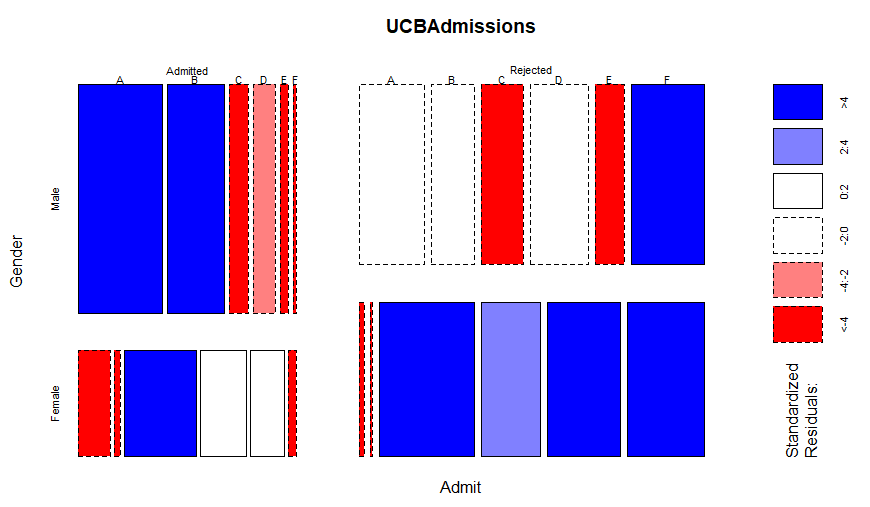
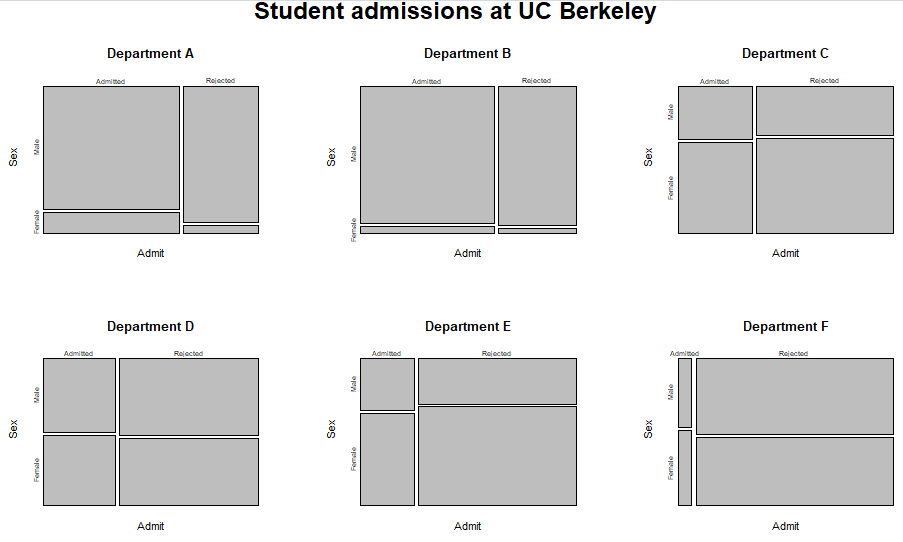
以前にもカテゴリカルデータの集計はやっているので、真似っこでやってみました。最初はモザイクプロットですな。自力でやってみた「カラフルな」やつを冒頭のアイキャッチ画像に示しました。
mosaicplot(UCBAdmissions, shad=TRUE) x <- apply(UCBAdmissions, c(1,2),sum)
冒頭のアイキャッチ画像はカラフルではあるものの、学部毎の集計については、成り行きなのでかなり見ずらい感じです。学部を無視して、男女別の合格者、不合格者を集計してみたものが以下に。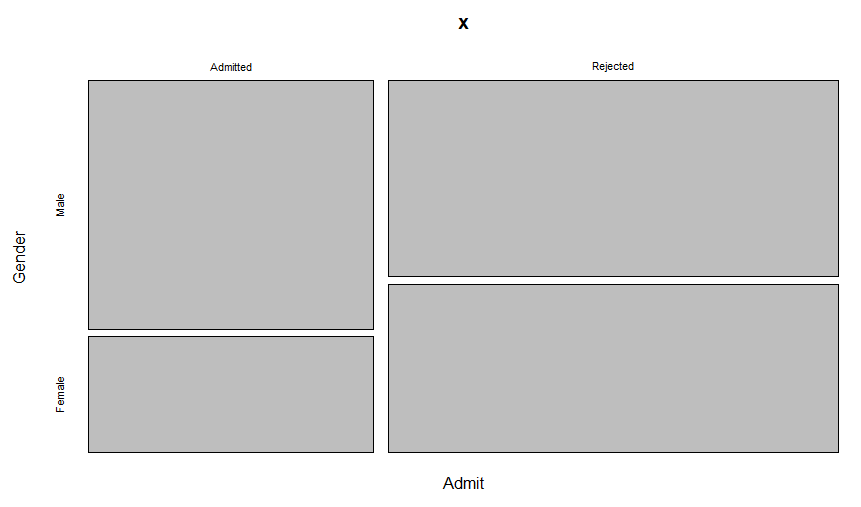
上のグラフを見ると「なんだ、女子学生の合格率の方が低いじゃん。アメリカも50年前は男女差別(どこかの国はいまだにある?)あったのね」という印象を受けてしまいました。しかし、どうもここに「シンプソンのパラドックス」があるみたいです。
例題の処理例
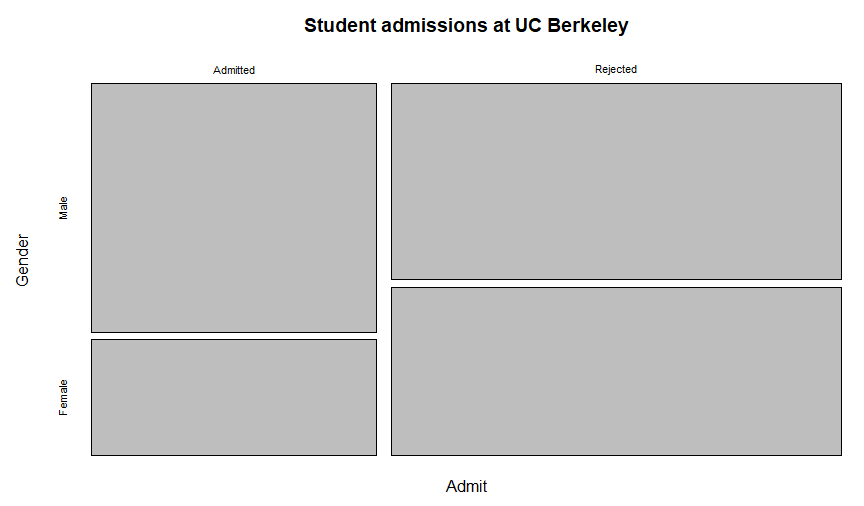
そこで解説ページに書かれていた処理例をそのまま実行してみました。処理例でも最初はapply処理後のモザイクプロットです。なんだ、自力でやったのと同じじゃん。解説ページの方はタイトルが付いているケド。。。
上記の処理例の結果が以下に。
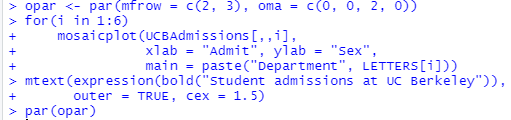
しかし、上記で止まっていた自力更生とは異なり、処理例では問題の「学部毎」の集計に踏み込んでいっています。処理のコードは以下のとおり。
学部AからFの結果のプロットが以下に。
これを見ると、性別で差がある感じはあまりしませんな。それどころか、学部でいうとA、B、D、Fでは女子学生の合格率の方が男子より高いし、合格率が低めのC、Eでもその差は微妙。女子学生の方が成績が良いような気がしてきます。
しかしapplyで学部の欄を押しつぶして、全体でみると男子学生の合格率が高いです。その理由の多くが
-
- 合格率が高く(入り易い)学部A、Bで男子学生の志望者が圧倒的に多い
- 一方合格率がやや低め(難しい?)学部C、Eでは女子学生の志望者が多い
ためじゃないかと思います。男子諸君は入り易い学部で大量入学を果たし、女子学生は難関学部に挑戦した志望者が多かった分不合格者も多かったという感じでないかと。
これがシンプソンのパラドックスっすか。知らんけど。