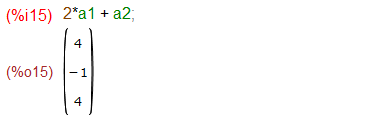今回は、前回と「違う問題」なのだけれどMaxima上で行っている処理はといえばほぼほぼ同じ。でもま、やらないことには先に進まないのでほぼほぼ同じようなことをダラダラ実施。そんなんで良いのか?良いわけないですが。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の参考書(以下URLは「改訂9」)の「改訂1」版の演習問題をMaximaの練習用に使わせていただいております。
数学の御本なのに数学の勉強には全然なってないです。恐れ多いことです。すみません。
今回の問題
ザックリまとめると『3ベクトルで生成される部分空間Wの基底と次元を求めよ』ということなんであります。
3ベクトルは以下の3つです。例によってリスト表現を列ベクトルに改めるのにtransposeしております。
さて部分空間W(R3)の元 x(ベクトル)は、上記3つのベクトルと c1, c2, c3∈Rなる定数をつかって
x = c1 * a1 + c2 * a2 + c3 * a3
という具合に書けると。[a1, a2, a3]の形の行列Aのrankを求めれば自由度、そしてWの次元 dimWが分かると。こんな感じで良いですか?
次元は2みたい。c1, c2, c3と置いたけれども自由度3-2で1とな。前回もやった処理方法を繰り返してみます。
上記は自由度1なのでc3=1としてみた(計算しやすいから)の場合。一応検算してみると。
よってc1 * a1 + c2 * a2 + c3 * a3 = 0 は
-2*a1 – a2 + a3 = 0
から a3 = 2*a1 + a2。再び検算。
a3 は、a1とa2で書けてしまったので、線形独立なa1とa2がWの一組の基底となり、Wの次元 dimW は 2 である、と。知らんけど。なんかグダグダだなあ。