R言語所蔵のサンプルデータをABC順(大文字先)で端から眺めております。今回は1970年代の米国における事故死者の統計6年分です。前回に続き時系列データです。前回のガスの消費量に季節変動があるのは素直に納得できるのでありますが、事故にも季節変動があることが明らかな感じです。なぜ?
※「データのお砂場」投稿順Indexはこちら
今回のサンプルデータセットの説明ページは以下です。
Accidental Deaths in the US 1973-1978
ただし上記ページを見ても処理例など書かれておらず、それどころかデータに関する説明もほとんどありません。データの出典が書かれているくらい。よって今回は完全自力で処理を進めるしかありません。しかし、今回「も」時系列データなんであります。前回の時系列データ処理の方法をそのまま真似すればOK?
まずは生データ
生データをロードしてその素性(時系列データ=Time-Series)を眺めたところが以下に。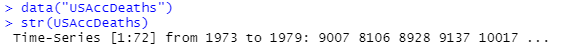
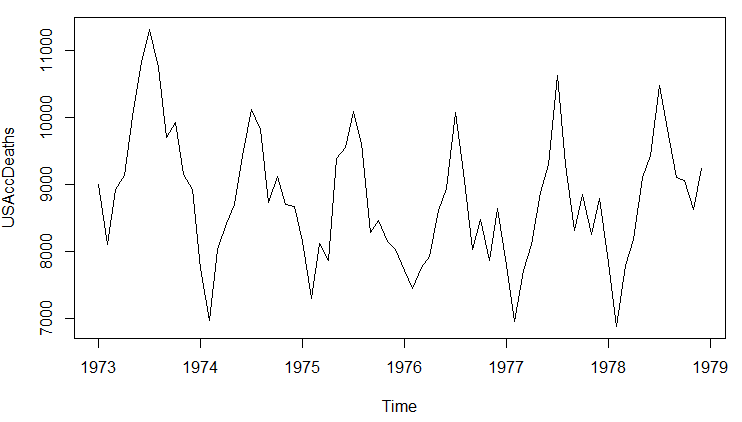
上記をみると高々72点のデータであるので全体を見てみると以下のよう。
数字が全てお亡くなりになった方だと思うと気の重い上記テーブルですが、統計のサンプルデータだと言い聞かせればそんなもんかと。上記テーブル見るだけで「季節変動」がある感じが分かりますな。
時系列プロットを行わせるコマンドと念のため開始点、終了点、freqency(年間のデータ点数)の表示が以下に。
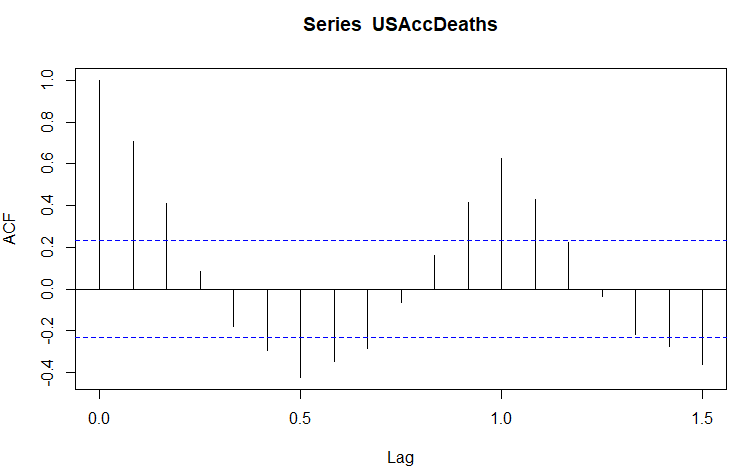
季節変動の様子は、acf (自己相関)をとれば明らかになるかと。コマンドは以下です。
acf(USAccDeaths)
生成された自己相関のグラフが以下に。Lag=1.0(年)で相関が高くなっていることが分かります。毎年同じパターンが繰り返されているってことですな。
STL使用した処理
前回STLという処理を行って、季節変動と、トレンド、そしてそれ以外の残差にデータを分解することができました。今回も同じ処理を行ってみたいと思います。
STL=Seasonal decomposition of Time series by Loess
みたいです。しかし Loess も分かりませぬな。
Loess=Locally Estimated Scatterplot Smoothing
だそうな。まあ、これを使えば時系列から季節変動、トレンドなどを分離できると。
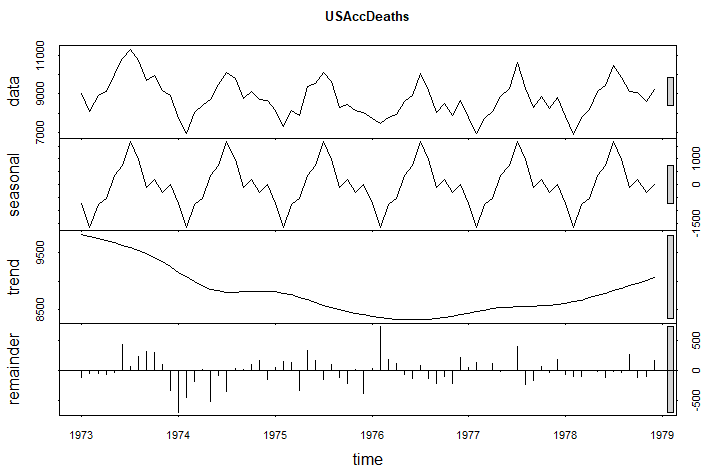
work <- stl(USAccDeaths, s.window="per", robust=TRUE) plot(work, main="USAccDeaths")
s.window=”per”のperはperiodicだと。季節変動を抽出するときの周期お任せってこと?robust=TRUEにするとLOESSをつかったロバストなフィッティングになるのだそうな。なんだか分からんですなLOESS知らないと。
グラフが以下に(アイキャッチ画像と同じもの)
見事なといったらバチがあたりそうな季節変動のパターン。そしてダラダラさがり、また増加に転じるトレンドであります。
これまた処理は出来たですが、分かったような分からぬような。