『やっつけな日常』シリーズの中に押し込めていた『RustにいればRustに従え』シリーズ独立であります。頭の固い(C頭と呼称します)年寄には敷居の高いRustをなんとか使えるようになりたいとの一念です。その初回はありがちな数値積分です。Rustらしく、mut無、for無で積分をやっつけました。どうよ。
※『RustにいればRustに従え』関係記事 index はこちら
※動作確認は、Windows11のWSL2上にインストールしたUbuntu20.04LTS上のrustc 1.64.0 (a55dd71d5 2022-09-19) で行っています。
トートツに数値積分(定積分)
唐突に数値積分やってみたのは、別シリーズの記事
忘却の微分方程式(81) 反復練習44、級数の和の極限値、Maxima
という回で、無限につらなる筈の級数が簡単な定積分になることをこの目で見たためです。思いつきました。Rustのイテレータを使えば、一撃で数値積分できるんじゃね、と。定積分に帰着した後の式とその積分結果(Maxima様による)は以下です。
つーことは、この定積分の値を4倍してやればπになるんじゃね。
Rustで数値積分にしてみる
Rustで書くからには当然ともいえる努力目標があります。
-
- mut (可変な)変数は「なるべく」使わない
- forとか繰り返しなどは「なるべく」使わない
上記の制限の元、上のような定積分を数値積分でやっつけよう、ということであります。数値積分のアルゴリズムは数値積分の中でも簡単な
中点則
を採用させていただきました。区間の中点の値に区間の幅を掛けて積算するだけのもの。簡単でお楽。はるかな太古の時代、大学初年のFORTRANの授業でやった気がします。当時のマシンは大型機、今も忘れない Univac1106。
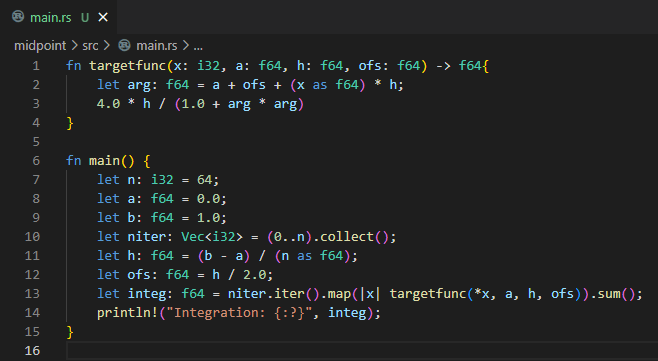
さて作成したRustのソースコードが以下に
fn targetfunc(x: i32, a: f64, h: f64, ofs: f64) -> f64{
let arg: f64 = a + ofs + (x as f64) * h;
4.0 * h / (1.0 + arg * arg)
}
fn main() {
let n: i32 = 64;
let a: f64 = 0.0;
let b: f64 = 1.0;
let niter: Vec<i32> = (0..n).collect();
let h: f64 = (b - a) / (n as f64);
let ofs: f64 = h / 2.0;
let integ: f64 = niter.iter().map(|x| targetfunc(*x, a, h, ofs)).sum();
println!("Integration: {:?}", integ);
}
mut使ってない、Loopも無し。淡々と let しているだけで数値積分できる筈だと。
実機での実行結果
実行してみました。黄色の矢印の先をご覧くだされ。円周率3.141まではあっているみたい。ま、そんなものかい。
Rustのイテレータの威力凄まじいっす。