前回は媒介変数表示、今回は極座標表示です。どんどんメンドくなっているようでいて極座標表示での積分はお楽でした。本当か?しかしそのプロット、それも極座標表示のグラフ2つに挟まれた隙間の面積部分、塗りつぶし方がわからないっす。苦し紛れに手で塗りました。グラフの塗りつぶし方の練習も必要ね。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
塗りつぶし方はマニュアルに書いてあるものの
Maxima様は抜かりなく、プロットの塗りつぶしにも対応しています。以下のMaximaの日本語マニュアルページへ行けばサンプルもあり。
サンプルはこんな感じ。
でもねえ、今回の極座標表示の曲線2本の「隙間」を塗るという技にはたどり着きませなんだ。修行が足りんな。
極座標表示の曲線
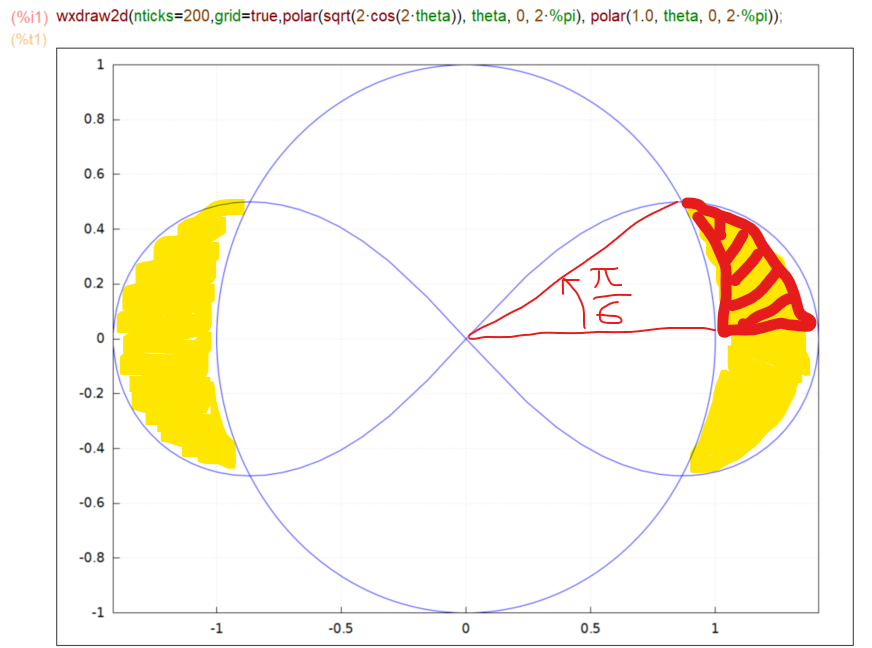
さて、今回の問題は以下のプロットの黄色い部分の面積を求めよというものであります。円 r=a そして r^2=2*a^2*cos(2Θ)、教科書によればレムニスケートと呼ぶのだそうな、に囲まれた面積であります。aの値を決めないとプロットできないので、以下では a=1としております。よろしゅう。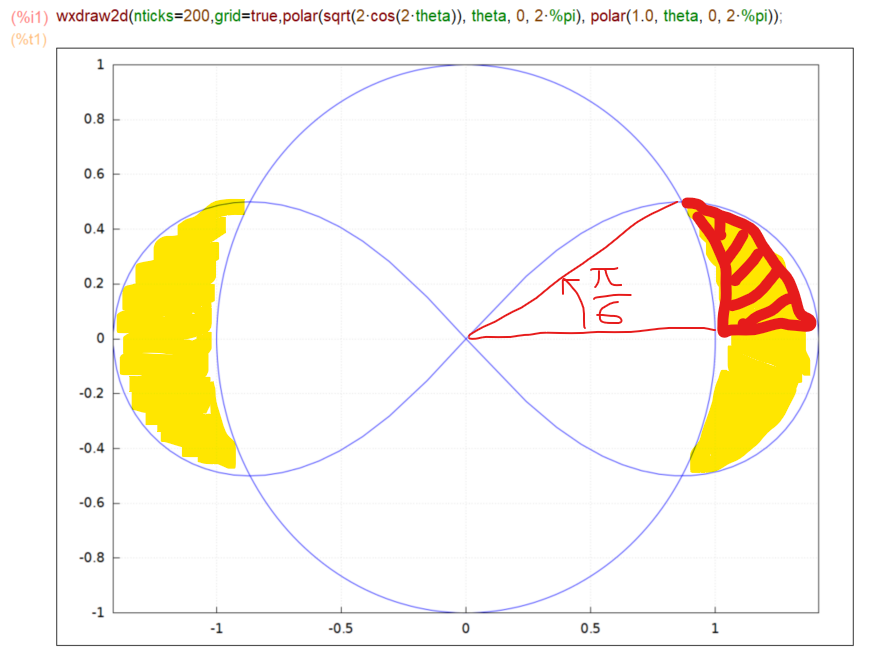
本当は黄色い部分をMaxima様に塗りつぶしていただきたかったのですが、今回は手作業でお茶を濁してます。さらに言うと原点対称の図形だけに赤で「ハッチング」した部分、第1象限ってやつ、の面積を求めてそれを4倍すればよろしかろう、という方針であります。
さて、極座標(r, Θ)に関して方程式 r=f(Θ)上の点Pについて、点Pに対応するΘがαからβまで増加するとき線分OPが通過する面積Sは以下であると。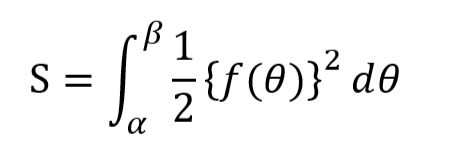
なんだ、結構簡単じゃん?
まずは交点(第1象限)求めるところから
上記のプロットでは既にπ/6とΘの値を書き込んでありますが、これを求めるのはこんな感じ。R0が円、R1がレムニスケートの式であります。
方程式をsolveに与えると、いくつか解が失われるけれどいいのかよ、と脅されましたが無視します。第1象限だもんね。
Θ=0からπ/6の範囲では、R1の方がR0より遠方を動いているので積分はこんな感じかと。積分の名詞形を味わったあと評価すればお答えが。なお、問題の面積はS(第1象限だけ)の4倍なのでevの中で4倍してます。
積分自体はすらすらできたんだけれども、プロットは難しいなあ。凡人は修行あるのみ?