前回は極座標表示での定積分でしたが、今回は3次元での求積です。なんだか難しくなってきた?でも、やってみると(正確に言えばMaxima様にお願いすれば)定積分は一撃でした。結局断面積を求める方がムツカシかった?それに3次元プロットのやりかた忘却してるし。ポリゴンぐりぐりしたいんですけど。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
今回は3次元だっ!
まあね、数学的に言えば2次元が3次元、面積が体積になっても大した違いはないのかもしれません。しかし忘却力の老人は既に3次元プロットの方法、すっかり忘れてます。以下の回で1度やってるのですが、その後、2次元平面で暮らしていたからなあ。
忘却の微分方程式(28) 3次元プロット、MathematicaとMaxima
いつもお世話になっております。Maximaの日本語マニュアルの該当箇所は以下です。
さて、今回の例題は、3次元空間内に以下の式であらわされる「楕円面」で囲まれる体積を求めよ、とのことです。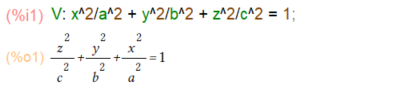
x, y, z のどれか一つに0をぶち込んでやると、x軸、y軸、z軸の軸上から眺めた図形が想像できますが、これは皆同じ、どっちから見ても楕円ということね。
3次元プロットを行うためには、a, b, c に何か具体的な数をアサインしないとMaxima様に描いていただけないので、以下のようにしてみます。ありがちだな。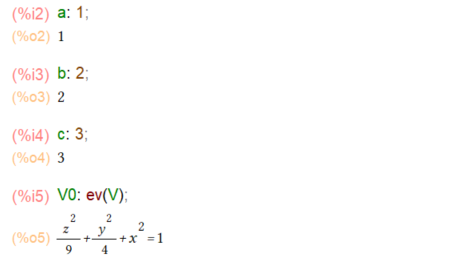
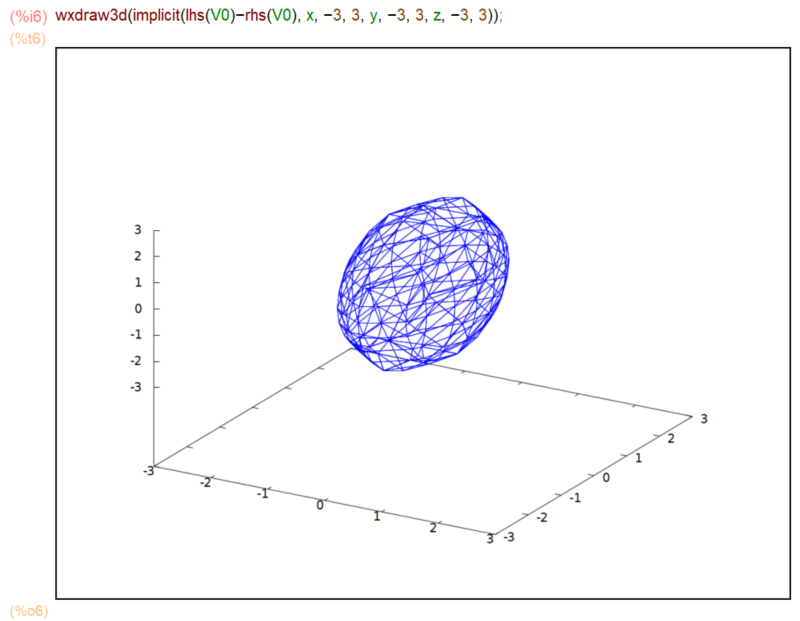
Maxima様の draw3d()関数のimplicitでは、チョメチョメ=0の形(チョメチョメ部分だけでもよい)を入力しなければならないみたいなので、左辺から右辺を引いたものを与えて、まずはwxMaximaのwxdraw3d()関数でプロットしてみました。冒頭のアイキャッチ画像のとおり、3次元プロットはできました。しかし
ポリゴンぐりぐり(古い)、できないじゃん
いつもはwxMaximaのラッパ関数(wxMaximaのウインドウの中にグラフを表示してくれる)で満足しているのです。しかしwxMaximaの中に表示されるのは静的な画像でグリグリすることはできません。今回は3次元なので上下左右いろいろな方向から見たいです。
そこで本来のMaxima関数draw3d()を直接呼びます。
draw3d(implicit(lhs(V0)-rhs(V0), x, -3, 3, y, -3, 3, z, -3, 3));
こうすると、Maxima様の「下請け」で働いているらしい Gnuplot様のウインドウがアカラサマに現れてきます。こんな感じ。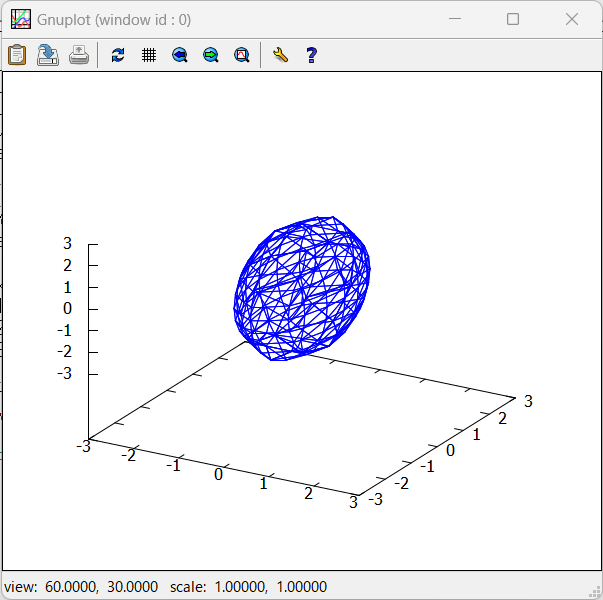
そしてGnuplotのウインドウ内では、マウスでドラッグすれば、「ポリゴンぐりぐり」的な各種回転などを行わせることができるのであります。こんな感じね。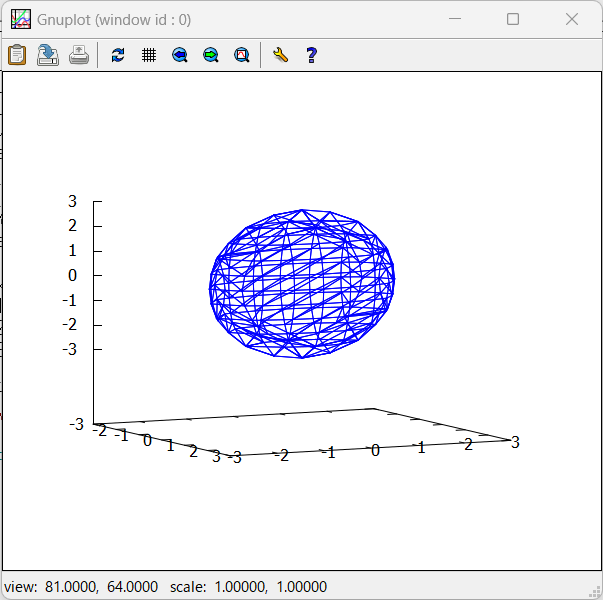
そして、x=0(X軸上)から眺めた場合が以下に。縦がZ軸、横がY軸っす。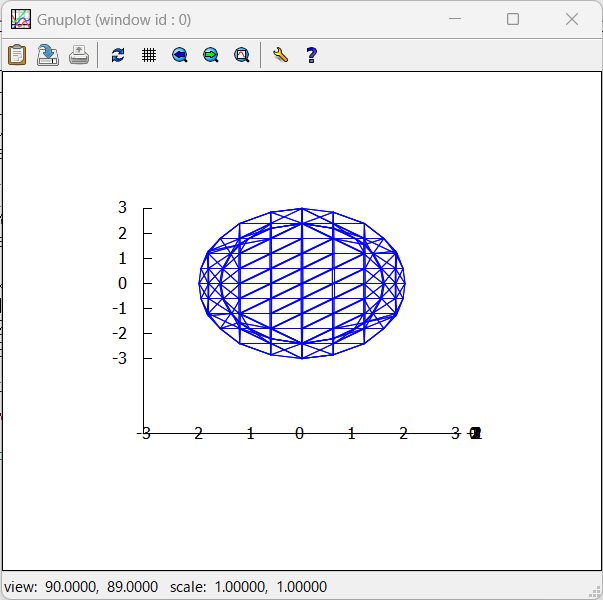
楕円だわな。あたりまえか。
断面積Sから体積Vを求める
さて断面積Sがxの関数として書けるならば、x=aからbまで断面が動いてできる体積Vは以下の定積分で書けるのは自明?ホントか。テキトーなこというなよ。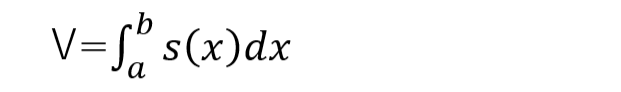
さて、今、x=0のx軸上から断面を眺めているのでその断面は以下の式であらわされる楕円だと。そしてその断面積は以下のように書けるっと。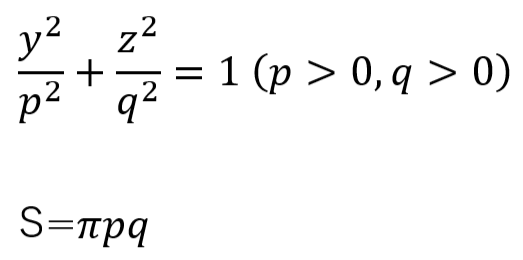
これだけ覚えていたら計算は出来る筈。まずは、後でゴタゴタ言われないように、a, b, c が正の数だと表明しておきます。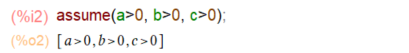
そして断面の楕円を表す式を x=t のときのtをパラメータとして書き直します。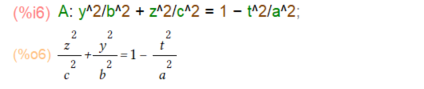
上の式を変形して、上の公式のp, qが計算できる形にするには、両辺を右辺で割ればよいと。右辺は1に決まってる、左辺も計算するとこんな感じ。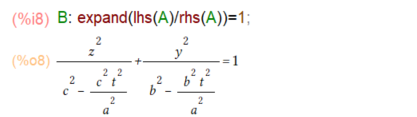
ここから p, q を求めると、上の式の左辺から、y^2項の係数およびz^2項の係数(coeff)をそれぞれ求めて平方根をとり、因数分解してやると整理した綺麗な形にできると。こんな感じ。
上で、p, q が求まったので、断面積Sはtの式として書き直せますな。そのSをt=-aからaまで定積分すればお答えが求まる筈。
求まってしまいました。なんだ、定積分、最後の1行で完了か。