前回、実際に時間波形に対してフィルタ処理を行うfilter関数の内部「相当のハズの」ブロック図を描きました。お惚け老人的には腑に落ちた感じ（ホントか？）今回は実際に「時間波形」をIIRフィルタしてみます。フィルタ係数は「アナログフィルタ」との関係性がつけやすいと思われる iir() 関数（第１２３回）で求めてみます。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上のScilab6.1.1およびScilab上のツールボックスを使用させていただいております。
今回のフィルタ
いつもLPFばかり実験していたので、今回はBPF（バンド・パス・フィルタ）してみます。フィルタ設計関数 iir() には以下のように指定してみました。
-
- 次数１１次
- バンド・パス(BP)
- バタワース特性(butt)
- 下限カットオフ（正規化周波数で）0.15
- 上限カットオフ（正規化周波数で）0.25
Scilabの場合、正規化周波数はフツーにサンプリング周波数を１とする計算です。偉大なるかなMatlab様はナイキスト周波数を１としていたハズ。コマケー話ですが。
実際にフィルタを設計し、その周波数ゲイン特性をグラフにするためのコードが以下に。
Fs=1000;
FcL=150;
FcH=250;
n=11
hz=iir(n, 'bp', 'butt', [FcL/Fs, FcH/Fs], [0 0]);
[hzm,fr]=frmag(hz,256);
clf();
plot2d(fr'*Fs,hzm')
xtitle('IIR BPF(Butterworth)');
xgrid();
xlabel("Frequency (Hz)");
ylabel("Gain");
上記の特性グラフが以下に（正規化でなくFsかけて実周波数に戻してます。）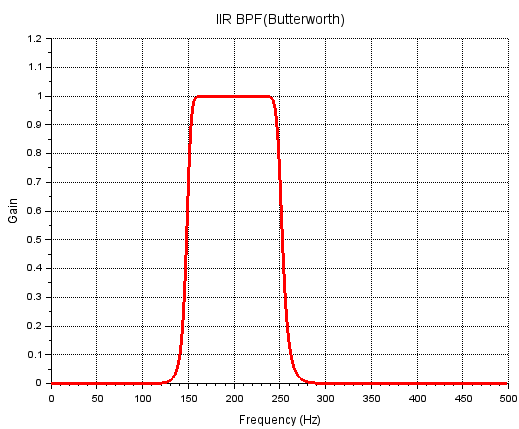
なお、設計関数 iir() が生成してくれたフィルタの伝達関数の実物が以下です。
ここに列挙されている係数共が、前回のブロックダイアグラムの三角形に入るかと思えば感慨深いっと。大丈夫か？
テスト用波形の準備
さて、実際にフィルタにかける時間波形を生成せねばなりませぬ。今回はアリガチな感じ。
-
- 101Hzの正弦波
- 203Hzの正弦波
- 305Hzの正弦波
気持半端な周波数にしたのは、キリをよくすると時間波形がテキパキしすぎるので、ちょっと「唸る」ような感じにしてみました。
上記の波形を生成して確認するのに自前関数 genSin と plotFFT2 を使ってます。そいつらのソースは以下の回においてあります。
手習ひデジタル信号処理(119) Scilab、fsfirlinのLPFでフィルタしてみる
なお、上記回では FIRフィルタの設計関数の fsfirlin を使って似たようなことをしてます。テスト用の時間波形を生成するコードが以下に。
nSample=4096; F101=101; F203=203; F305=305; [t, y101]=genSin(Fs, nSample, F101, 0, 1); [t, y203]=genSin(Fs, nSample, F203, 0, 1); [t, y305]=genSin(Fs, nSample, F305, 0, 1); wavT = y101 + y203 + y305;
以下は生成した wavT波形の一部を拡大したもの。「うねり」見えてますか？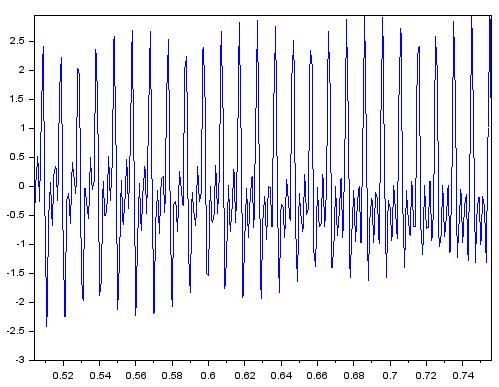
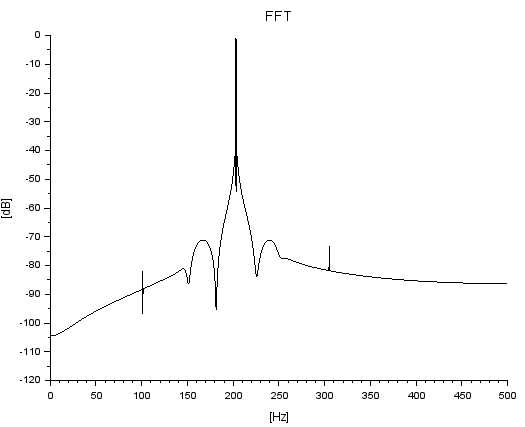
また、自前関数 plotFFT2でのFFTプロット（周波数軸は実周波数になっている）が以下に。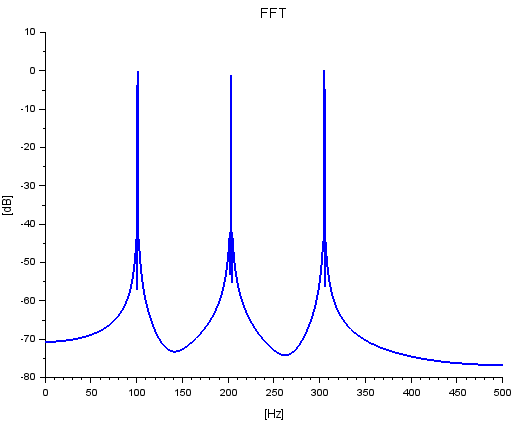
101Hz、203Hz、305Hz付近にピークがあります。予定通り。
いざやフィルタせん
フィルタかけるのは filter関数で一撃。
[y, zf] = filter(hz.num, hz.den, wavT);
さてフィルタ後の時間波形 y をプロットしたものが以下に。
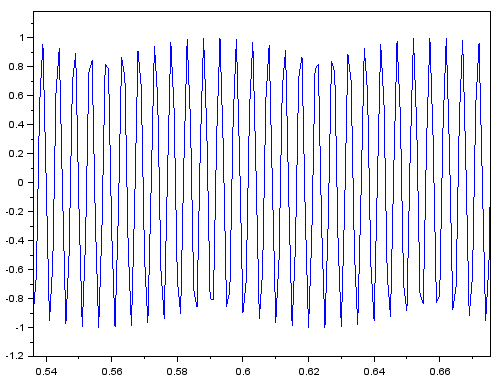
まあ200Hz付近の波形にみえると、ちょっと「唸り」が残っているけど。
FFTかけてみるとこんな感じ。
200付近が残り、100付近と300付近に「わずかに」ピークが残っているけど、そんなもんかい。