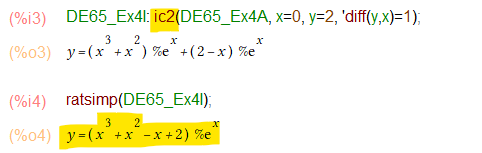前回につづき定数係数2階非同次線形微分方程式です。今回はその初期値問題。教科書的にはステップバイステップでお教えいただいております。こちらでは伝家の宝刀 ode2() 関数で一般解を求め、ic2() 関数で初期値を与えれば初期値問題も一撃デス。折角、初期値を与えて関数の形が確定したので今回はプロットもしてみましたぞ。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版? そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
ic2関数
ode2関数で求めた一般解に対して、初期条件(独立変数のある1点における従属変数の値およびその時の1階微分の値)を与えて微分方程式を解くのがic2関数のお役目です。既に以下の過去回にて「同次形」については練習済です。
忘却の微分方程式(139) 反復練習102、2階同次線形微分方程式の初期値問題、Maxima
Maximaマニュアル(日本語版)の関係ページが以下に。
例題
例題では、非同次方程式の右辺Q(x)は多項式と指数関数の積の形です。しかし ode2() におすがりする場合は何も考えずに微分方程式を定義して与えるのみ。こんな感じ。
上記の黄色のマーカのところに一般解が登場してます。いつものことながら一撃。
さて初期値問題を解く場合、ic2()関数に以下を与えねばなりません。
-
- 一般解
- 独立変数(今回はx)の値
- 上記の時の従属変数(今回はy)の値
- 上記の時の一階導関数の値
なお、ic2()から得られた素の形のままだと教科書的にはちょっと手抜きな感じなので、最後 ratsimp()にお出まし願って整理したものが黄色のマーカ部です。
オマケ、例題の解のプロット
初期値問題ということであれば、初期値後のxの値を変化させてyがどうなっていくの?ということが当然気になる筈。ということで以下のようにしてプロットしてみました。初期値を与えた点 x=0 から 2までだけれども。
plot2d(rhs(DE65_Ex4Y), [x, 0, 2])
プロットするとこんな感じ。も少し複雑な形状が良かったのだけれどもシンプルで単調に増加。グングン伸びてるなあ。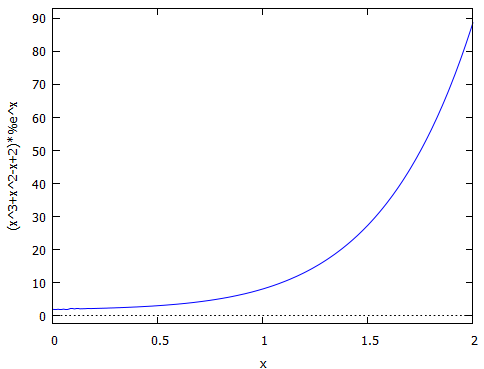
プロットもできたし、まあ、いいか。