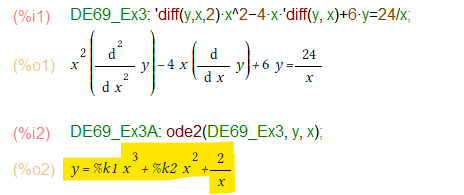ずっと「定数係数」の微分方程式ばかり練習（解いたのはMaxima様）、「変数係数」のときはどうよ？という疑問あり。解けん？しかし、変数係数微分方程式でも「オイラーの微分方程式」というものは「変数変換」によって定数係数に帰着させて解けるぞよ、とのお教えであります。当方は伝家の宝刀ode2()にお願いするばかりなんだが。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
オイラー(Euler)の微分方程式
さてオイラーの微分方程式（２階）は以下のような形です。
当然、オイラー様のお名前を冠する方程式が２階限定なんてことはなく、ずっと上の階まで続いておるらしいのでありますが、以下の事実により２階まで限定とさせていただきます。
伝家の宝刀、ode2()関数は２階まで
切れ味鋭い（全部お任せで済む） ode2()関数ですが、マニュアルにも２階までと明言されています。それより上の場合、過去回では desolve()関数使って、ちょっとメンドイことやってました。
今回の例題
教科書的には、独立変数 x を x=etのように変換して解いていくのですが、ode2()にお願いする場合は、何も準備は要りませぬ（まあ、内部で良きに計らってくれるみたいデス。）こんな感じ。
お惚け老人には自力じゃ絶対に解けん微分方程式っすけど、ode2()なら一撃。とくに今回はいつものお約束の後始末もなし。即、教科書的にもＯＫな一般解の形でもとまりました。なお、%k1、％k2はMaxima様の任意定数です。境界値問題の解き方は前回練習した通り。
教科書的な「解法」がある形、ode2()はほぼほぼパーフェクトな感じ。