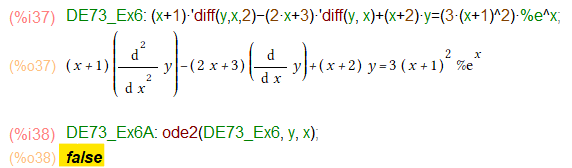前回は「変数係数」の微分方程式でも「オイラーの微分方程式」というものは変数変換で解ける（でも ode2で一撃よ）の回でした。今回も「変数係数」の微分方程式なのですが、ついに「ode2で一撃」の神通力は通じないこととなりました。教科書では「階数低下法」による解法を解説くださってます。教科書通りに一歩一歩解くしかないのか？
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
階数低下法
階数低下法が何気にずるいのは「同次方程式の０でない解の一つ」が分かったならば、という前提があることです。それを手がかりにズルズルと非同次な方程式の一般解に至る道筋を教科書では説明いただいております。結構メンドイです。お惚け老人は、途中間違わないで手順を実施できる自信はまったくありませぬ。
だいたい同次方程式の０でない解の一つが求まっている、ということ自体、出来すぎな気がしないでもないです。だいたい変数係数なんだし。ムツカシーです。
今回の例題
今回の例題の変数係数２階線形微分方程式は以下です。
(x+1)*y”-(2*x+3)*y’+(x+2)*y=(3*(x+1)^2)*ex
毎度のことですが、自分じゃゼッテー解ける気がしません。
とりあえずそのまま ode2 と desolve にぶち込んでみる
いつもなら伝家の宝刀 ode2 で一撃のハズがこんな感じ。
一言、falseとな。ode2は各種の解き方を網羅しているものの、「何もヒントもない」上記の形は分からんということみたい。。。
ままよ、ということで desolve にも御出馬いただきました。
こちらも敗退。
同次方程式の解を一つ求めるところ
例題の左辺は以下です。
(x+1)*y”-(2*x+3)*y’+(x+2)*y
ここに付け入る「隙」があるのでした。もしy”=y’=yであれば、変数係数(x+1)-(2*x+3)+(x+2)は0じゃのう。。。
なんだ、y”=y’=yであるような関数であれば上記左辺＝０の同次方程式の解になれるのね。そして、y”=y’=yであるような関数はお惚け老人でも知っています。つまり「同次方程式のひとつの解Y1(x)」は、ex ね。確かめてみると以下の通り。
その先は ode2 で一撃よ
同次方程式の解のひとつ、ex が求まったので、非同次方程式の一般解 y0(x)はu(x)*ex とおけます。これで元の微分方程式を u(x)を使って書きなおすことが可能。教科書では書き直した後「ごちょごちょ」とやって２階を１階におろして一歩一歩解いていくのです。しかし u(x)で書き直したら ode2()復活。一撃でu(x)が求まりました。u(x)が求まれば、求める一般解はそれに ex を掛けてやったらええ、と。
緑マーカのところが一般解です。ヒント一つもらえたら壁も乗り越えらた？乗り越えたのは Maxima様ですが。