インピーダンスの計算をMaxima様にお願いするとか、ましてやLTspiceに御出馬いただくなど牛刀割鶏の類、とは思います。手計算がメンドければ電卓あるだろ～。でもね、忘却力の年寄は電卓を使ってもチョイと複雑になるともういけません。あれ手が滑った？結局は計算をお願いすることになるんであります。しかし、一長一短あり。
※「SPICEの小瓶」投稿順インデックスはこちら
※ Analog Devices, Inc. LTspice を使用させていただいて動作確認しております。今回使用のバージョンは以下です。
XVII(x64) (17.0.37.0)
Maximaによるインピーダンス計算
お惚け老人は、別件シリーズにてMaxima様にお世話になっております。無償にて使用可能な定番の「数式処理ソフトウエア」であります。線形代数だろうが、微分方程式だろうが、お惚け老人が計算する程度の「初等な数学」の問題であれば一撃で解ける優れものです。当然ながら複素数など屁でもありません。実数でも複素数でもインピーダンスの計算など一撃。ホントか？
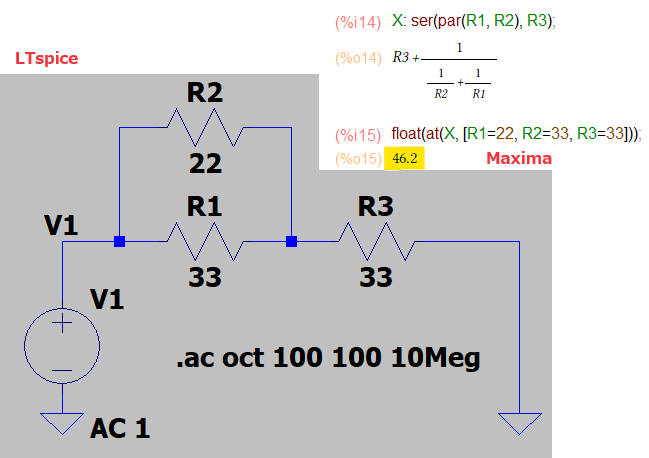
例えば以下は、抵抗R1とR2が並列（par）に接続されているものに直列(ser)に抵抗R3が接続されている全体をXとおくもの。「数式処理ソフトウエア」なのでこのような文字変数のままでも式を計算できるのが強みです。そして次の行で具体的な数値を各文字変数に当てはめて(at) 結果を浮動小数点型で求めてます。こんな感じ。
46.2Ωとな。
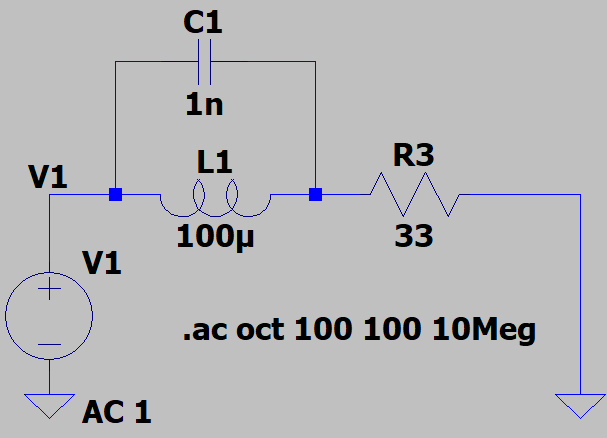
コンデンサ（キャパシタンス）やコイル（インダクタンス）が含まれる場合も同様に計算できます。以下はR1の代わりにC1、R2の代わりにL1を置いたもの。キャパシタンスにはci、インダクタンスはiiという関数で与えてます。まあね、Maxima様は数学系のソフトなので、虚数単位はjではなく、%iなのがちょっとね。これまた同じ方法で文字変数どもに値を与えれば、float型で答えを得ることができます。こんな感じ。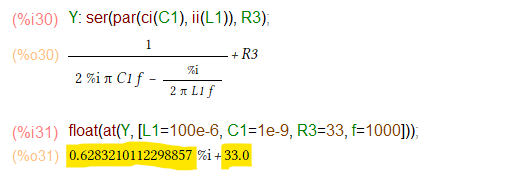
なお、流石に Maximaに最初から、serだの、parだのいう関数が定義されている筈もなく、そいつらは「お手製」であります。定義はこんな感じ。
define(ser ([Lis]), '(apply ("+", Lis)))$
define(par ([Lis]), '(1 / (apply ("+", 1/Lis))))$
ci(C):= 1/(%i*2*%pi*f*C)$
ii(L):= %i*2*%pi*f*L$
ser/parは可変個引数とれるようになっているので、直列に長くなろうと、並列に多数になろうと、組み合わせは無限、ホントか？
まあ文字で書いた式をまず解いてというときにはMaxima方式はお役立ちかと。
牛刀割鶏、LTspiceでインピーダンス計算
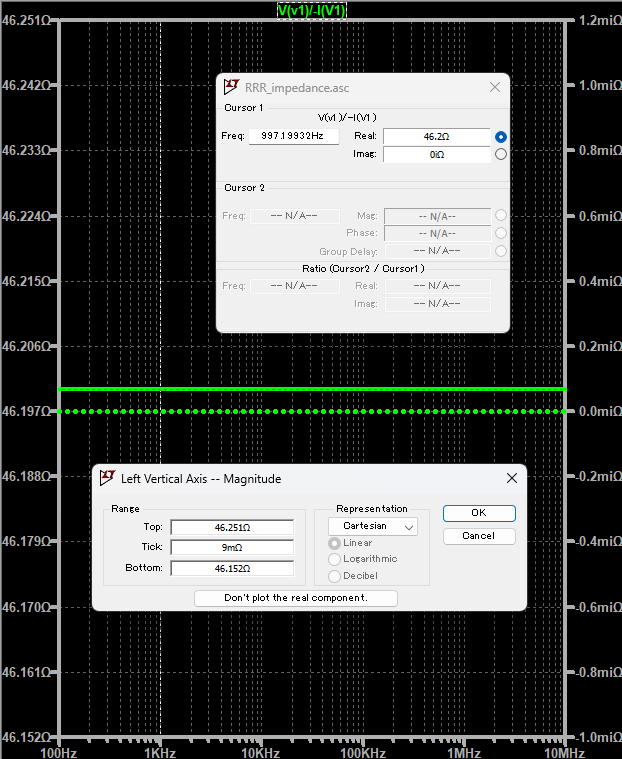
一方、LTspiceでもインピーダンスを計算できますな。なんといっても回路シミュレーションにつなげられるので、どうせ後で回路図描くなら計算していただくのもありかと。まずは最初の抵抗３個の例。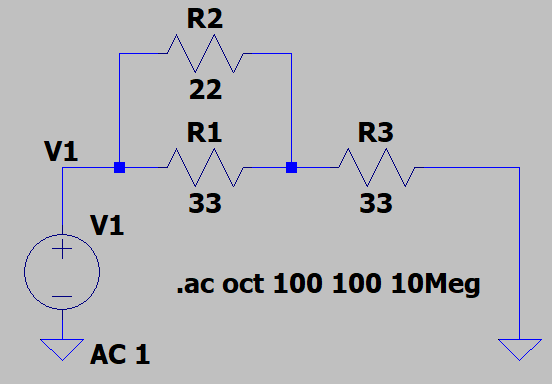
これをシミュレーションした結果が以下に。
Realの欄に、インピーダンス46.2Ωが表示されております。ミソは
V(v1)/-I(V1)
を計算するところ。電圧を電流で割っているので縦軸は「Ω」表示となります。このときRepresentationのところを「Cartesian」指定しておくと、真っ平な上記のグラフなどには適するかと。
続いてLとCを並列に置いたもの。
シミュレーション結果が以下に。
黄色のマーカで印した Real と Imag のところ、先ほどMaxima上で求めた値とほぼほぼ一緒だ。計算できとるようだね。
ちなみに共振点付近の波形が以下に。
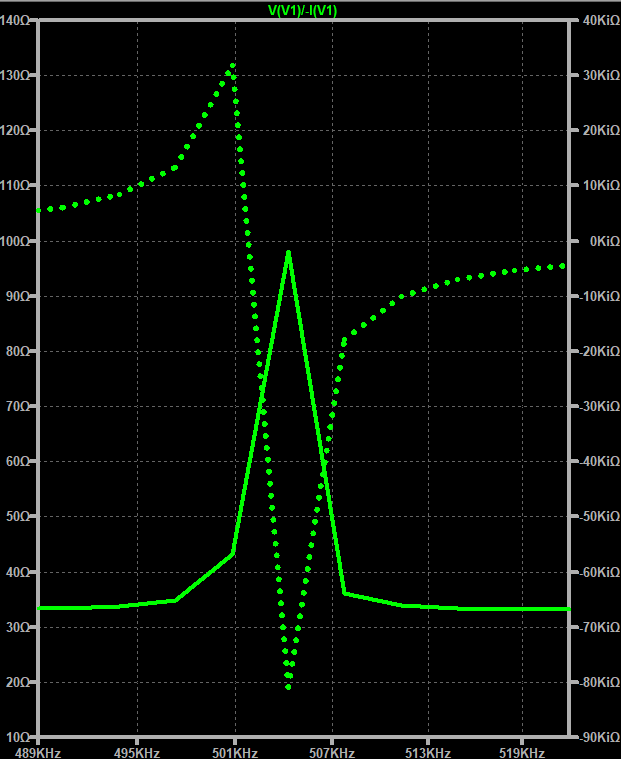
勿論、Maximaでもグラフは描けますが、どうせシミュレーションするならLTspiceの方がお楽？どっちもどっちか。