
前回 Maxima on Android(MoA)の再活用ということで、2次元平面上のベクトルを1次変換した後のベクトルと合わせてグラフ表示できるようにしてみました。ここまでは数学ですが、ついつい抽象から離れて具象化したくなるお惚け老人です。複素インピーダンスをベクトル表示できるんじゃね。やってみました。
※「やっつけな日常」投稿順 Index はこちら
合わせ技の今回
今回は、2次元ベクトルのグラフ表示を行った前回の以下の記事と
やっつけな日常(70) Maxima on Android 再活用、ベクトルの表示と1次変換
別シリーズでMaxima様にインピーダンスの計算をお願いしてしまった以下の記事を「合わせれば」ほぼできてしまうものです。手抜きだな。
SPICEの小瓶(44) LTspiceでインピーダンス計算、Maximaでも計算、どっち?
計算(表示)サンプルケース
今回計算のサンプルとしたのは、以下のようなR、L、C「そろい踏み」の回路の複素インピーダンスです。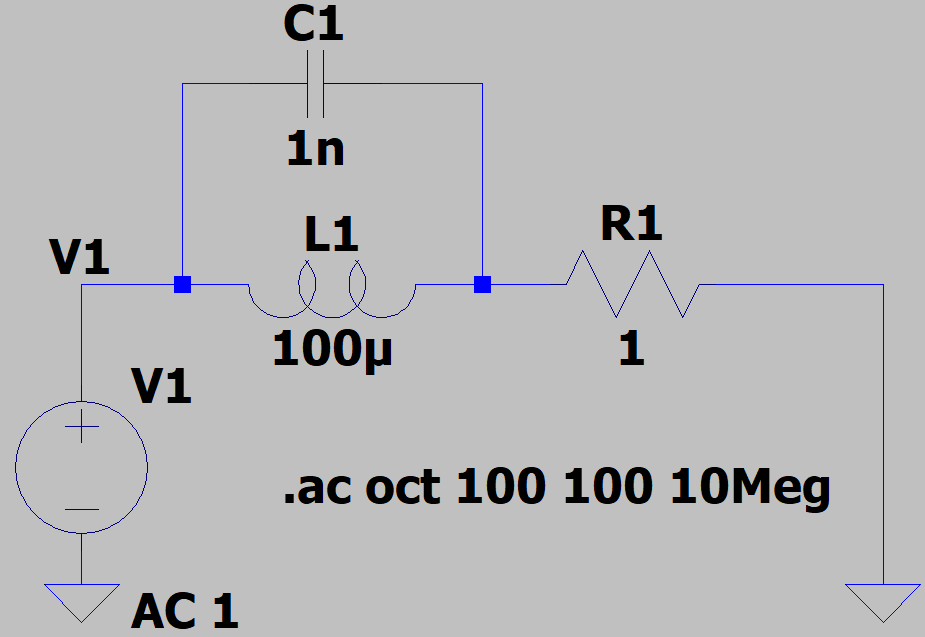 以下はLTspice回路図っす。
以下はLTspice回路図っす。
上記をシミュレーションした結果が以下に。黄緑の実線は複素インピーダンスの実部で、点線は虚部です。Y軸はΩになるようにしてあります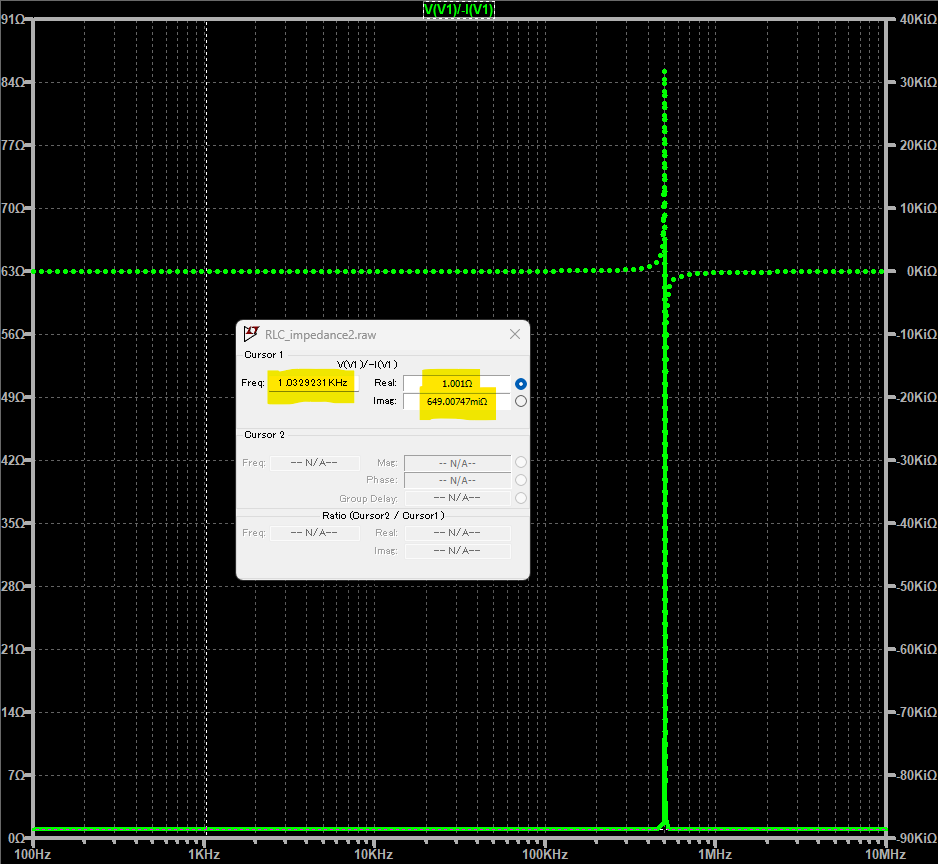 。
。
カーソルを「ほぼ」1kHzのところに置いたときの、実部は約1Ω、虚部は約650mΩと読み取れます。これが今回のホンワカした目標値デス。
MoA上での結果
まずは上記回路の1kHz時の複素インピーダンスのベクトル表示から。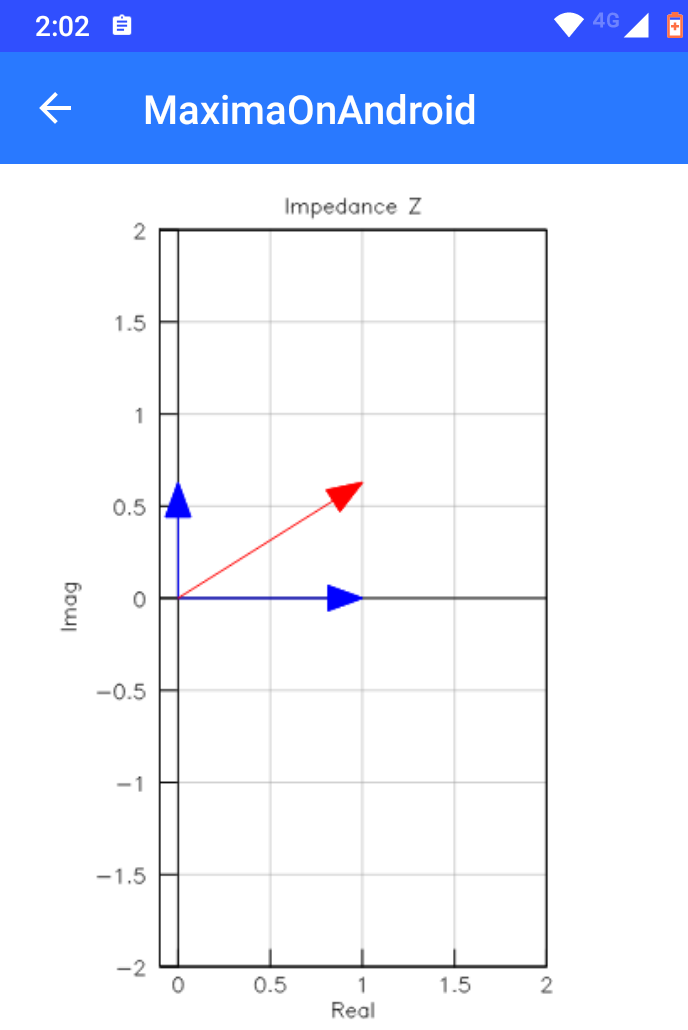
ベクトル表示できているようです。上記の裏側で行われている計算が以下に。
黄色のマーカーのところで、C1、L1、R1から出来ている回路を定義し、黄緑色のところで具体的な定数を当てはめて数値として計算。その結果を青のところでプロットという流れです。
Maximaのソース
パソコン上のMaximaでもスマホ上のMoAでも同一のソースです。必要な関数定義が上の方に並んでいますが、スマホ上で「編集」する必要があるのは Example のところの回路を定義するZの行と、具体数値を当てはめるZfの行だけです。ここを必要に応じて変更し、MoA上でバッチ実行すれば解が得られます。
/* Maxima BATCH FILE 2024/05/20 J.Halfmoon */
/* Display impedance vector */
algebraic:true$
/*- Utilities -----------------------------------*/
log10(x) := log(x)/log(10)$
roundF(x, p) := float(round(x*10^p)/10^p)$
dB(Vout, Vin) := float(20*log10(Vout/Vin))$
vec2(x, y) := matrix([x],[y])$
mat22(a11, a12, a21, a22) := matrix([a11, a12],[a21, a22])$
vecP(v2) := vector([0, 0], [v2[1, 1], v2[2, 1]])$
vecLis(lis) := if listp(lis) then map(vecP, lis) else [vecP(lis)] $
vi: vec2(1, 0);
vj: vec2(0, 1);
I: mat22(1, 0, 0, 1);
/*- impedance calculation -----------------------*/
define(ser ([Lis]), '(apply ("+", Lis)))$
define(par ([Lis]), '(1 / (apply ("+", 1/Lis))))$
ci(C):= 1/(%i*2*%pi*f*C)$
ii(L):= %i*2*%pi*f*L$
/*- plot impedance vector ------------------------*/
plotImp(vP1, vP2, xR, yR) := draw2d(
xrange=xR, yrange=yR, proportional_axes=xy,
xaxis=true, yaxis=true, grid=true,
title = "Impedance Z",
xlabel = "Real", ylabel = "Imag",
color = blue, head_length = 0.2, head_angle = 20,
color = blue,
vecLis(vP1),
color = red,
vecLis(vP2)
)$
prSub(z) := ceiling(max(realpart(z), imagpart(z)) * 1.2)$
plotImpedance(z) := block([tmp],
tmp: prSub(z),
XR: [-0.1, tmp],
YR: [-tmp, tmp],
vZ: [vec2(realpart(z), 0), vec2(0, imagpart(z))],
vY: vec2(realpart(z), imagpart(z)),
plotImp(vZ, vY, XR, YR)
)$
/*- Example -------------------------------------*/
Z: ser(par(ci(C1), ii(L1)), R1);
Zf: float(at(Z, [C1=1e-9, L1=100e-6, R1=1, f=1000]));
plotImpedance(Zf);
複素インピーダンスのベクトル表示ができるのなら、次はボード線図も描くべきだな。ずるずると抽象から離れてドロドロな現物に向かう年寄。