前回、教科書が「行列の対角化を利用して一階の連立微分方程式を解くの回」だったのに、こちらはMaxima様のdesolve一発で解いてしまいました。今回の教科書は「行列を対角化できなくても固有値が一つあれば解けるの回」です。やはりMaxima様にお願するときはdesolve一発です。そんなのバカりだな。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書の例題をMaximaの練習に使わせていただいております。ただし御本家『培風館』様のホームページで検索してみるも掲載されていないようです。絶版？ そのため以下のリンクは『Amazon』の通販ページであります。ご注意を。
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
今回の例題
今回の例題の形は、以下再々かかげます式のAの行列を「対角化できん」場合です。
といって制約はあり、Aを対角化できないとは言っても固有値に重解を持つので固有ベクトルは求まると。
しかし当方は desolveに丸投げデス。問題は以下に。
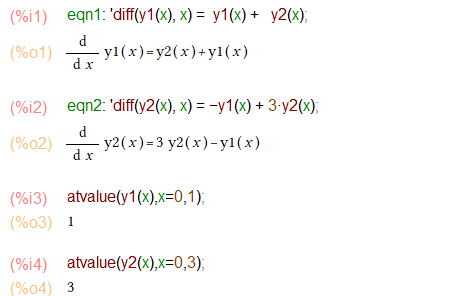desolveには「相性のいい」境界値問題です(atvalueで具体的な数字を定義できるので、後始末がお楽。）
例題の解
desolve一発で「ほぼほぼ」OKではあるのですが、教科書的には「e2xでくくれ」よという感じです。結果をratsimpに渡してみます。
黄色のマーカーのところが解、これなら教科書的にもOKっと。
次回からはちょっと応用問題？ ホントか？