前回は、基礎を踏み固めるべしとて、Scilabの離散１次元畳み込み、conv関数などを練習しました。１次元をやったのだから、次は２次元だよね、という流れで今回は離散２次元畳み込みのconvol2d関数練習してみます。改めて眺めてみると１次元のときとはスタイルが微妙に違うんでないかい？ひと手間かけろと？
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上のScilab6.1.1およびScilab上のツールボックスを使用させていただいております。
離散２次元畳み込み
AI（ニューラルネット系？）を見たらば離散２次元畳み込みの大群（ビッシリ詰まった感じ）に遭遇必至であります。そういうとき、パディングとかストライドとかいろいろパラメータはあろうかと。しかし、Scilabのデフォルトで使える離散２次元畳み込みのconvol2d関数にはそういうパラメータはありません。素のままね。といいつつ１次元のときにあった「定義通り」に計算するconv関数に相当する関数は不在。常にFFTつかった「裏口」から計算するconvol2d関数のみであります。裏口とは人聞きの悪い。大量データの処理にはFFT使う方法の方が早いからでしょう。でも正面からと違い、計算結果は微妙。最後にひと手間かける必要があるみたいです。
まずはconvol2d関数の処理の様子が以下に。
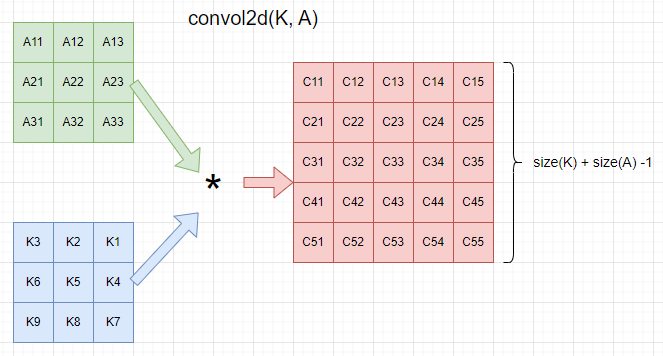
処理対象データAに対して、フィルタカーネルKを作用させているイメージです。処理結果は常にAよりもsize(K)-1だけ大きくなります。この辺は重なりが１のときから結果が出ていた１次元のデフォルト（full)のときとは見た目がチョイと違いますな。結果が出るのは上記のKのようなカーネルだとK5に相当する場所であると。そう思ったら一緒か。
ただし、前回練習した１次元のconvのようにsameとかvalidにあたるオプションはないです。必要ならば自ら取り出せということか。
ScilabのHELPページが以下に。
convol2dを使用してみる
上記のHelpページに水平方向のソーベルフィルタ（水平方向のエッジを検出する）を適用する例があがっていたので、まずは３ｘ３サイズのソーベルフィルタの定義から。
sobelH = [1 2 1; 0 0 0; -1 -2 -1]
実行したところが以下に。３ｘ３の行列ができとりますな。
対するに５ｘ５サイズのデータ（オール１）に上記のソーベルフィルタを適用してみます。処理は以下のようです。
A5 = ones(5, 5) C5 = convol2d(sobelH, A5) C5C = clean(C5) D5C = C5C(2:6, 2:6)
５ｘ５サイズのデータＡ５にconvol2dをつかってソーベルフィルタをかけ、C5という結果を得てますが、先に述べたとおりC5のサイズは７ｘ７サイズです。「裏口」からFFTベースで係数求めた連立方程式を解いている筈なので本当はスッパリしたゼロになる筈のところでも何か小さな値が入ってます。そこで cleanという関数を適用してとても小さい数を強制ゼロにしてC5Cを求めてます。cleanはデフォルトで10-10以下だとゼロにしてくれるみたいです。さらに７ｘ７サイズの結果の中央部から「元画像」と同じサイズの５ｘ５サイズを取り出してD5Cを求めてます。
A5が以下に。
C5が以下に。とても小さい値がおりますな。
cleanして強制ゼロにしたものが以下に。スッキリ？
そして元データと同一の５ｘ５サイズを取り出し。
手順的にはこんな感じです。
上記のHELPファイルでは、元データの周りにあらかじめゼロ・パディングを施しておいて、上記とは異なるサイズの計算をした例が挙げられていたので、その方法も練習しておきます。雰囲気はこんな感じ。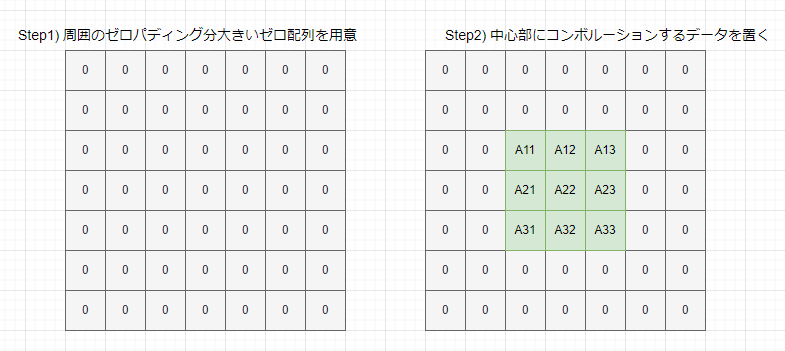
実際の処理手順が以下に。
A9 = zeros(9,9) A9(3:7,3:7) = 1 C9 = convol2d(sobelH, A9) C9C = clean(C9)
９ｘ９サイズのゼロ配列を作っておいて、その中央部にデータを詰めてからフィルタを適用してます。末尾の２行の処理結果が以下に。
２次元のコンボリューション関数は単機能な分、前後の手間がチトかかるっと。