長いこと繰り返してきた「反復練習」ですが、前回で教科書末尾に到達。お教えが身に付いたかどうかは別にして、一歩を踏み出さねばなりませぬ。今回からは「一歩踏み出した」グラフを描きたいと思います。使用させていただくのはplotdfパッケージです。これを使うと「ベクトル場を表示」できちゃうみたいです。知らんけど。
※「忘却の微分方程式」投稿順 index はこちら
※MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
plotdfパッケージ
wxMaximaのHelpブラウザを使えば、ローカル環境にインストールされた plotdfパッケージのHelpファイルを読むことができます。しかしWeb上で探したら、あまりヒットしてきませんな。ということで参照先URLとしては以下のページを貼り付けさせていただいてます。
https://maths.cnam.fr/Membres/wilk/MathMax/help/Maxima/maxima_68.html
なんかこの頃、おフランスにお世話になっている感じだな。
さてこのパッケージを使うと、以下のような形で表される「方向のある」場（２次元ですけど）をグラフにして表し、その上に「軌道」を描けます（境界条件を与えると、どこを通るのか解曲線を描いてくれるってことみたいです。）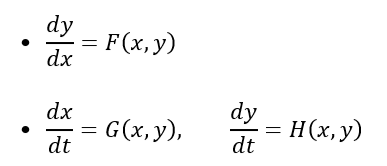
カッコいいです。１階だけ、と思っちゃいけないでしょう。ここで高校だか中学だかで習った物理を思い出せば、位置を微分すれば速度、速度を微分すれば加速度です。上記の２段目の方式で２式にバラせば２階の微分方程式も図時できるハズ。
まずは上記URLのHELPファイルを読みながら Example を動かしてみます。
さっそくロードから
手元のwxMaxima環境にplotdfのファイルはインストール済でしたが、ロード必要なパッケージです。こんな感じ。
わけもわからず最初の例を実行してみます。
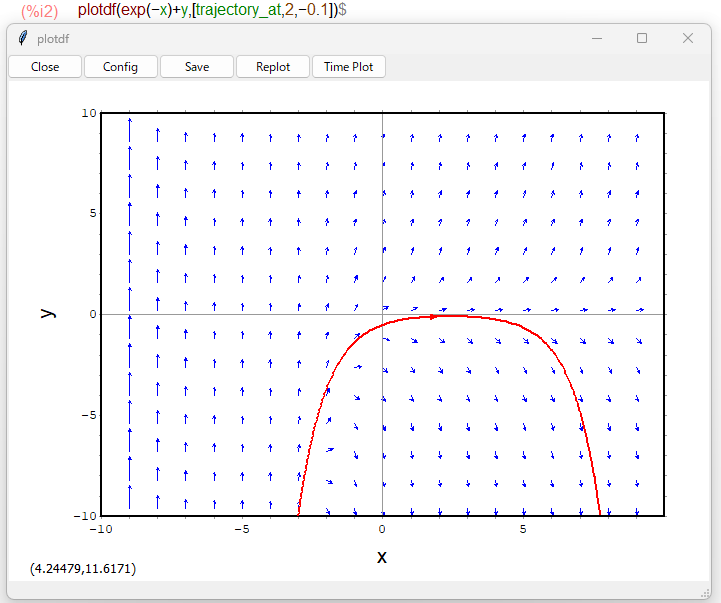
dy/dx = e-x + y とかける２次元のベクトル空間の(2, -0.1)を通る解曲線が上の赤みたいになるらしいっす。良く分からんなあ。
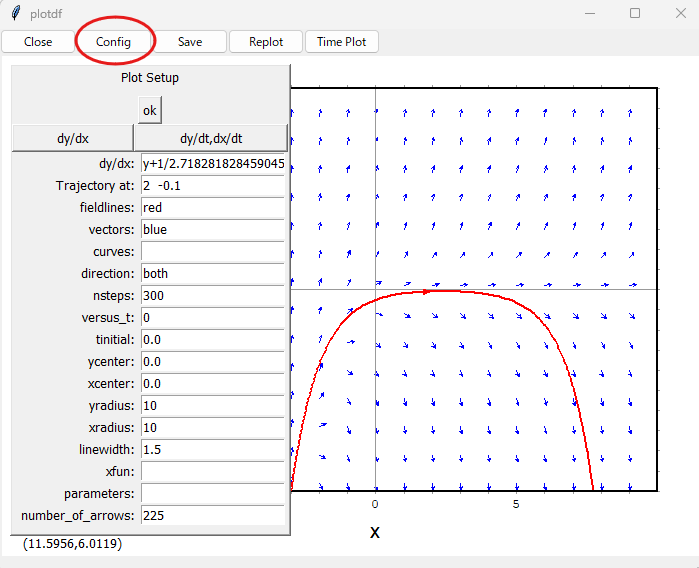
通常のプロットウインドウと違い、上の方にボタンが現れているので、闇雲にボタンを押してみます。
まずは config ボタンから。
いろいろ設定できるのね。
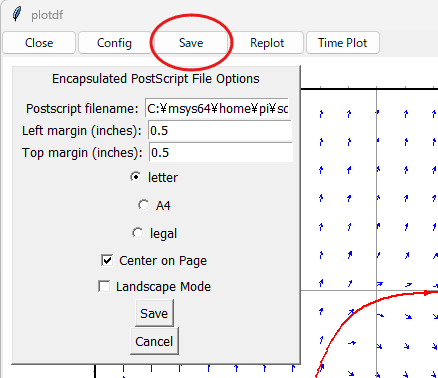
お隣のSaveボタンを使うとこんな感じ。EPS形式でグラフをファイル出力できるみたい。でも普段、お惚け老人はEPS形式使わんぞなもし。
呼び出しのときに与えた trajectory_at が気になるので、別の「点」を通してもらいました。こんな感じ。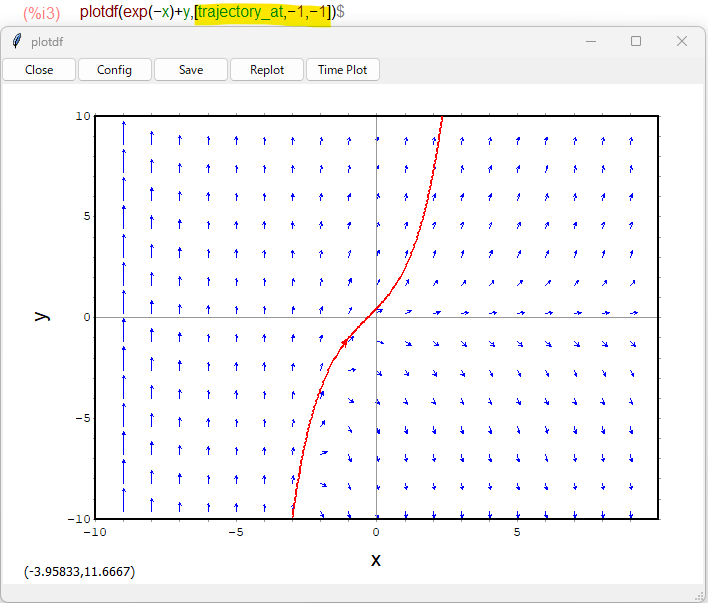
しかし、わざわざ入力パラメータを操作しなくても、表示ウインドウの上のテキトーなところをクリックしてやれば、そこを通る解曲線を描いてくれます。青丸は当方で書き加えたクリックした場所です。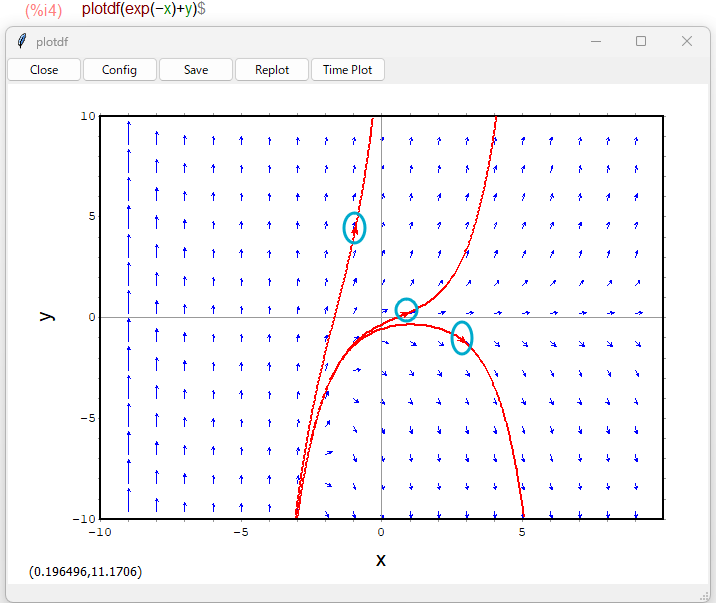
どうも、調子に乗ってクリクリやっていると沢山の解曲線が重なって醜くなるので、ときどきReplotするとクリアされてよい感じに戻ります。まあ、プロットウインドウの使い方は分かった感じ。ホントか？
位相空間？と時系列プロット
最後に Time Plotですが、これは今までみてきた「位相空間」でなく横軸時間の波形を描きだすものです。そのための例もありました。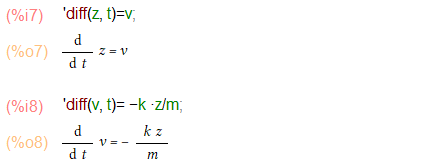
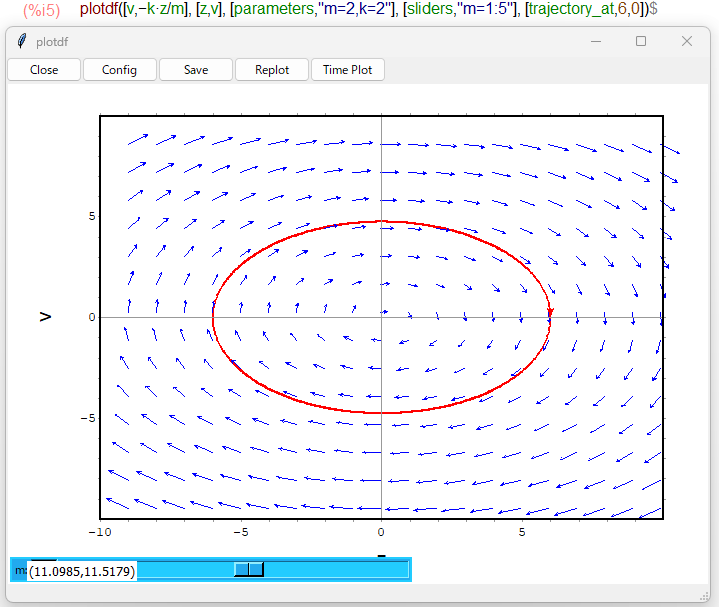
トートツに提示されても、お惚け老人にはなんじゃらホイという感じです。調和振動子である、と書かれてます。勝手に解釈すれば、
-
- zは１次元の位置（座標）を表す変数
- zを時間tで微分すれば速度v
- 速度vを時間tで微分すれば加速度、その加速度は -zに比例定数(k/m)を掛けたものに等しい。
- kはバネ定数、mは質量ってことでよかですか？
中学？高校でやる単振動（バネのみ）ってやつですな。えい。
縦軸が速度v 、横軸が位置z の「位相空間」っす。そして質量 m を「スライダー」で値を変えられるようになってます。ちょっとスライダーの位置、見難いんだが。横軸のzが隠れてしまっておるぞよ。
さて上にあるTime Plotボタンを押すと、ほれこのように。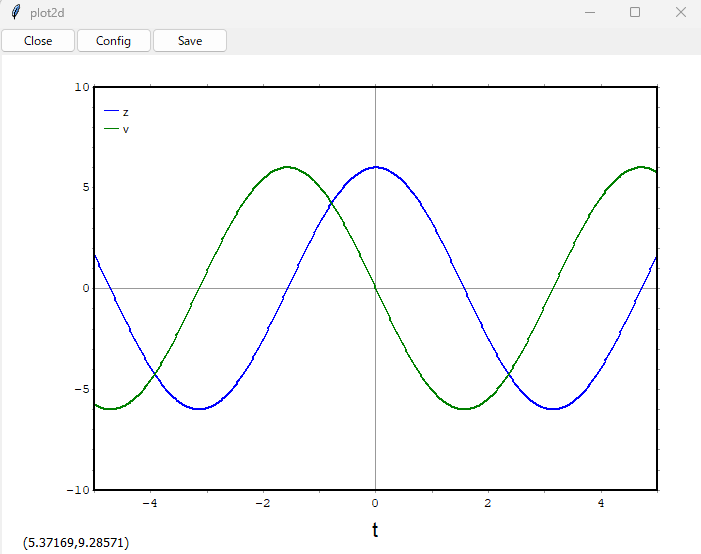
横軸は時間 t。正弦波が現れると何故か安心する年寄です。確かに単振動してますなあ。