前回まで『「なんちゃってな図」と「ほんわかした説明(数式なし)」により分かった気になる』を標榜しておりましたが改心いたしました。「数式にトートツに値を代入」、「なんちゃってな図」を描いて「もらおう」と。わかっちゃいないお惚け老人が真実に迫る唯一のよりどころは数式だと。まあ、ちゃんと描いて「もらえれば」なんでありますが。
※図(グラフ)を描くのをお願いするのは、別シリーズでもお世話になっておりますMaxima様です。皆大好き数式処理のフリーソフトウエアであります。
フェルミ準位とバンドギャップ
半導体を解説するページへ行ったらば、その冒頭に「フェルミ準位」、「バンドギャップ」などというお言葉が登場すること必定であります。勿論、お惚け老人がそれを説明しようなどと怖れ多いことはいたしませぬ。ちょいと検索するか生成AIにおたづねすれば大量な説明が見つかります。敢えてその中で今回実際に描いてみる「グラフ」の簡潔な解説として『OKAWA Electric Design(大川電子設計)』様の、以下のページを上げさせていただきたいと思います。
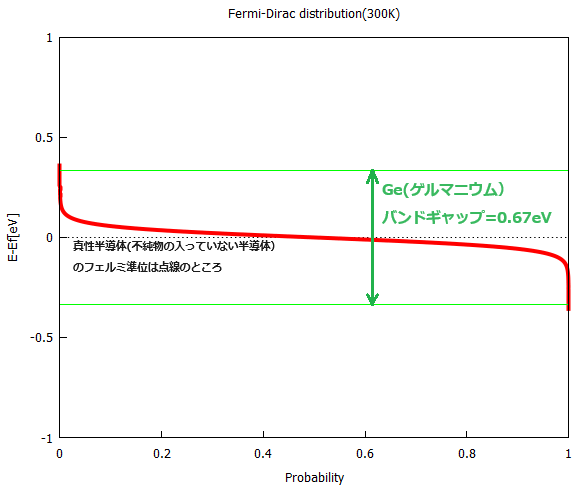
熱励起によってつくられる電子のエネルギー準位を縦軸に、横軸に存在確率をとって描いたグラフであります。そして「フェルミ準位」というのは、電子の存在確率が50%であるエネルギー準位であると。ただ、真性半導体(不純物の含まれていない半導体っす)におかれましては、そのまんまん中に禁止帯というものが走っており、下側の「価電子帯」と上側の「伝導帯」の2つのバンドに分断されております。そのギャップこそバンドギャップらしいです。
はてさて、フェルミ・ディラックの分布自体は以下の式であると。
よく登場する上記の式は、エネルギー準位Eを代入したら存在確率Pが求まるような公式っすね。でも描きたいのは、横軸が存在確率で、縦軸にエネルギー準位です。そこでMaxima様にお願いして上の公式を変形してもらいました。こんな感じ。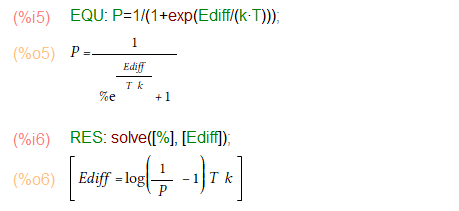
なお、E-EfのところをまとめてEdiffという1個の変数にしてしまいました。こうするとEdiff=0のところが、フェルミ準位ということになる筈。
さて、これでフェルミ・ディラック分布の「カーブ」が描けるハズなので、その上に書き込むバンドギャップを調べてみます。ありがちな半導体(真性)のバンドギャップ[eV]が以下に。
-
- Ge 0.67
- Si 1.11
- GaAs 2.45
- SiC 2.86
- GaN 3.4
真性半導体の場合、ギャップの中心にフェルミ準位がくるので、上記の値の半分を使えば価電子帯の上端と、伝導帯の下端が示せるハズ、多分。
描いたグラフ
通常ボルツマン定数は、
k: 1.380649e-23[J/K]
ですが、ここでの計算は eV単位なので、
k: 8.6171e-5[eV/K]
としてみました。温度はだいたい室温ってやつね。
T: 300;
描くグラフの式は以下です。
Ediff(P):=log(1/P-1)*T*k;
グラフを描くコマンドがこちら。
draw2d(
xrange=[0, 1], yrange=[-1, 1], xaxis=true, yaxis=true,
color=red,
line_width = 4,
explicit(Ediff(x), x, 0.000001, 0.999999),
color=green,
line_width = 1,
explicit(0.67/2, x, 0, 1),
explicit(-0.67/2, x, 0, 1),
xlabel="Probability",
ylabel="E-Ef[eV]",
title="Fermi-Dirac distribution(300K)"
);
グラフが以下に。
これみると、ほんの僅かに伝導帯に電子がいらっしゃるけど、残りは価電子帯にギュウギュウ詰めで動けん感じ? 列挙した中でバンドギャップが一番小さいゲルマニュウムでこれだから他の奴らはほぼほぼゼロ回答に限りなく近いっす。
なんか、自力(実際に計算したのはMaxima様ですが)で計算してみるとホンワカ分かった気がする(気がするだけよ。。。)