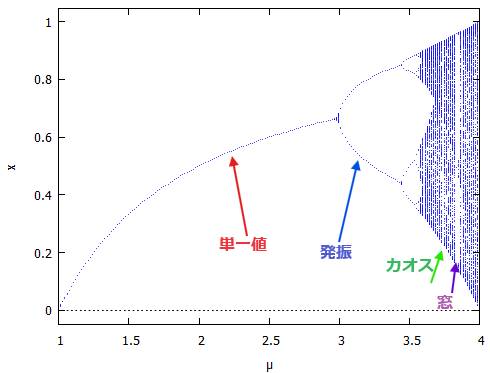
前回は「族に関する軌道図」を描くorbits関数でした。プロットされる軌道の中からカオスが湧きだし、拡大するとフラクタルになっておるっという不可思議。しかしそれを紡ぎだしているのは簡単な漸化式でした。今回はその漸化式の「発展の様子」を繰り返し方向にプロットしてみるevolution関数です。縦のものを横に見た感じ？
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
evolution関数
パラメータを含む漸化式に対して、横軸をパラメータにとって漸化式の取り得る値を縦方向にプロットするのが、前回のorbits関数でした。それに対して
x(n+1) = F(x(n))
のn=0から延々続く「発展の様子」をプロット可能な有限な範囲の横軸にnをとり、縦軸にx(n)をとってプロットするのが今回のevolution関数です。似たような処理なので、前回のorbits関数と引数は似ています。
evolution (F, y0, n, options, …);
Fに数列（漸化式）を与え、y0にn=0の時の初期値、nにプロットする最大繰り返し回数を与え、後は通常のプロットパラメータを与えるっと。
以下はevolution関数の説明があるMaxima文書（日本語）です。
プロット例
実際にプロットしてみるには漸化式が必用です。そこで、前回で「起動図」を描いている式を使うことにいたしました。
x(n) = μ * x(n-1) * (x(n-1) – 1)
前回描いたプロットを再掲します。
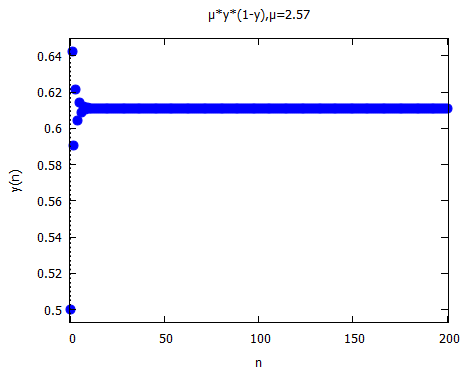
上記を参照しながら evolutionかけてみます。まずは、μ:2.57のとき。上記を見るに単一の値に「収束」する筈。
evolution(μ*y*(1-y), 0.5, 200, [title, "μ*y*(1-y),μ=2.57"]);
結果が以下に。最初バタついた後は予定通り収束。
さて、お次はμ:3.17;のとき、起動図を参照すれば、この辺では２点に発振するはず。こんな感じ。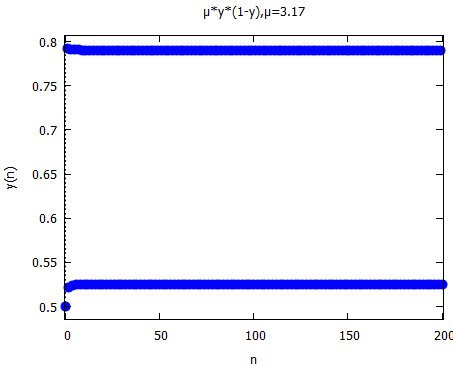
予定通り。
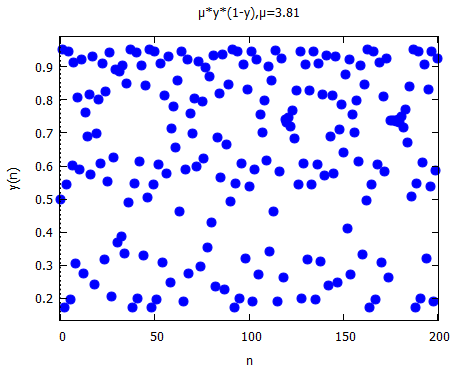
さてその次は μ:3.57; でどうよ。この辺はカオスになるはずじゃが。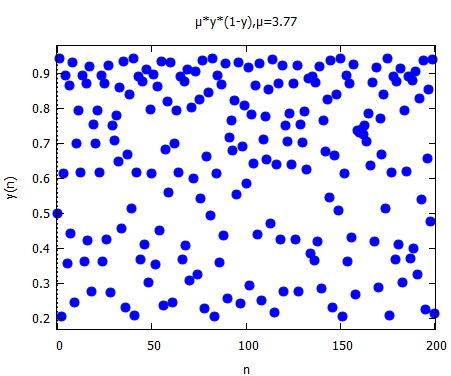
確かに、カオスな感じ。ほんとか？
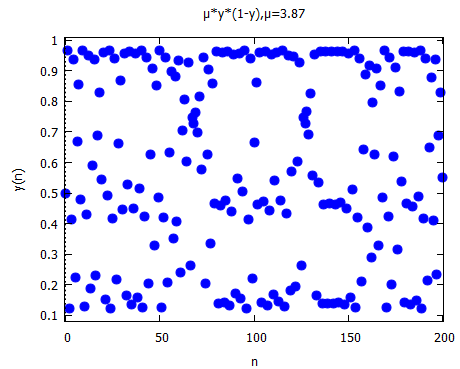
さてそれが、μ:3.84; などとしてみると如何に？あれあれ３つの値に収束してしまった。これが「窓」というものか？知らんけど。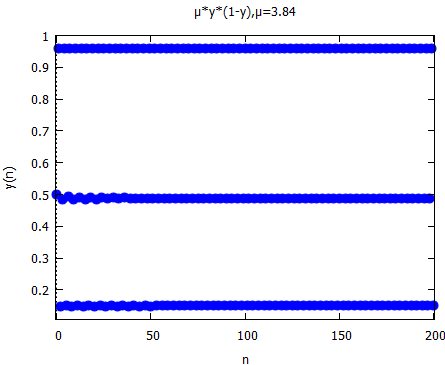
ところが、ちょいと下のμ:3.81;では、
ちょいと上のμ:3.87;では
変幻自在というか、カオスじゃのう。