前々回はorbits関数で「軌道図」を描き、前回は漸化式の「発展」をevolution関数で観察しました。そして今回は staircase関数で「階段図」です。前回、前々回同様、解析の対象は「再帰的に計算される漸化式」ですが表現の仕方で随分異なる様相が見えるような気がします。気がするだけですケド。。。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
staircase関数
dynamicsパッケージのstaircase関数の説明文書(日本語)が以下に。
https://flex.phys.tohoku.ac.jp/texi/maxima-ja/maxima_54.html
どうも「階段図」といっても、建築の世界の「そのものズバリの階段」からいろいろあるみたいです。しかしMaxima様のstaircase関数は、「再帰関係によって定義された数列」を描画することで「数列や関数の増加/減少を視覚化する」関数なんだそうな。
当然、3者とも引数は似ております。今回のstaircase関数はこんなかんじ。
staircase (F, y0, n, options, …);
ぶっちゃけ、関数名は違うけど、前回と引数はクリソツ。Fに数列(漸化式)を与え、y0にn=0の時の初期値、nにプロットする最大繰り返し回数を与え、後は通常のプロットパラメータを与えます。
先ずはゼロに向かって収束する等比数列の例
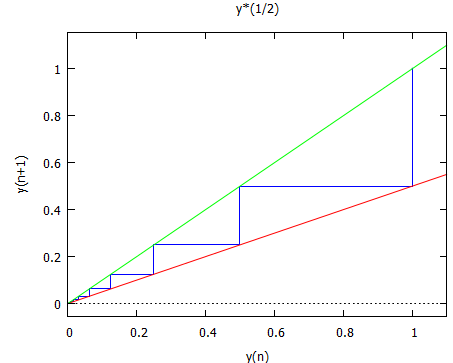
公比を1/2として、前の項に公比を乗じていけば単調に値は減少していきます。そんな様子を staircaseで描くにはこのように。
staircase(y*(1/2), 1, 11, [y, 0, 1.1], [title, "y*(1/2)"]);
まさに階段をゼロへ向かって下っていきますな。
三角関数ならどうよ
さきほどのMaxima様の説明文書では、三角関数 cos(y) を例にとってました。その場合のコードはこのようです。
staircase(cos(y), 1, 11, [y, 0, 1.1], [title, "cos(y)"]);
そして結果は、カクカクと曲がりながら奈落の底へと落ちていくっと。こんな感じ。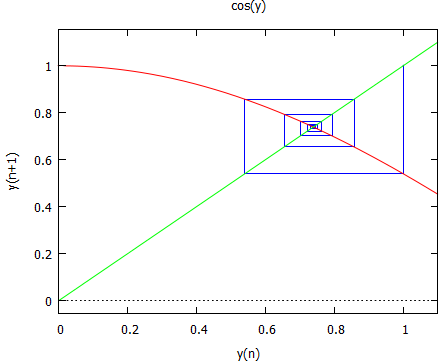
前回、前々回の漸化式ではどうよ
前回、前々回で登場した以下の漸化式の場合を描いてみます。
y(n) = μ*y(n-1)*(1-y(n-1))
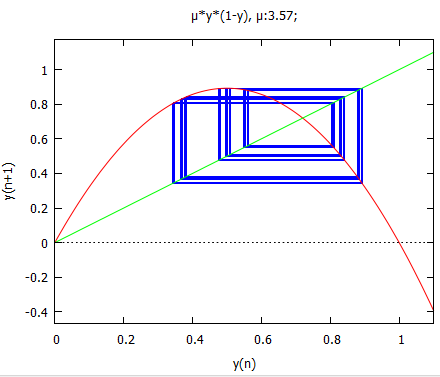
先ずは μ:3.57; のとき、前回、前々回の結果からカオス的な挙動をすることが分かってます。
staircase(μ*y*(1-y), 0.5, 100, [y, 0, 1.1], [title, "μ*y*(1-y), μ:3.57;"]);
カオスに見えたものは、一向に収束も安定もしないで回り続ける数列だったのね。
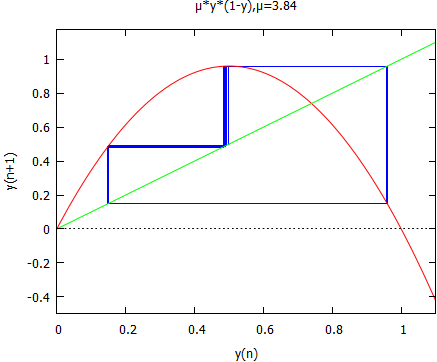
μ:3.84; ではどうよ。このときカオスの隙間にある「窓」にいるような。
ちょうどいい所で回っているので値が安定するのね。
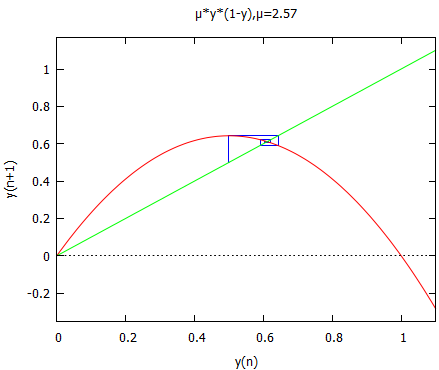
ちなみに μ:2.57; カオスにならず1点に収束する場合はどうよ。
ああ、確かに1点に向かって収束していく。。。
素人老人にも階段図は分かり易いデス。