第161回でevolution関数を使い「漸化式の発展」の様子を観察しました。今回はその2次元バージョン? evolution2D関数です。発展の様子を観察する対象は「連立漸化式」じゃないかと。ムツカシそうだよ。でもカオスでフラクタルな処理例はちょっとさらに上を行くのさ。ホントか?よくわからんが。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- Maxima 5.46.0(x86_64-w64-mingw32)
- wxMaxima 22.04.0
“dynamics”
このところ練習しておりますMaxima様のdynamicsパッケージです。この “dynamics” というお名前に、分かったような、分からぬような、腑に落ちなさをずっと感じておったのです。そしたらば『一橋大 川平友規』先生のお書きになった以下の文書読んで目が覚めました。ホントか?
忘却力のお惚け老人、読んだその場は目から鱗が落ちても、直ぐに元に戻ります。
evolution2d関数
evolution2d関数を含むdynamicsパッケージの説明文書(日本語)が以下に(以下は東北大様のサイトだと思うのだけれども、結構ダウンしていること多し。個人の感想デス。)
https://flex.phys.tohoku.ac.jp/texi/maxima-ja/maxima_54.html
第161回で練習した evolution関数と今回のevolution2d関数の引数を比較しておくとこんな感じです。
evolution( F, y0, n, ..., options, ...); evolution2d( [F, G], [u, v], [u0, v0], n, ..., options, ...);
evolution関数は、漸化式を
y(n+1) = F(y(n))
という形で表します。Fは「nは気にせずyの式で」定義。一方, evolution2d関数は、
u(n+1) = F(u(n), v(n))
v(n+1) = G(u(n), v(n))
という連立した形です。同様に「nは気にせず」FとGをそれぞれu、vで定義します。
evolution関数が横軸に n をとって縦軸に項の値を表示する形。それでnにつれて発展する様子を描くのに対して、evolution2d関数は横軸にu(n)、縦軸にv(n)をとって2次元的に発展の様子を描きます。順序をハッキリさせるため直線で点をつなぐと前回の階段図みたいな感じにもなります(直線でなくナナメ線なので階段にはならんけど。)
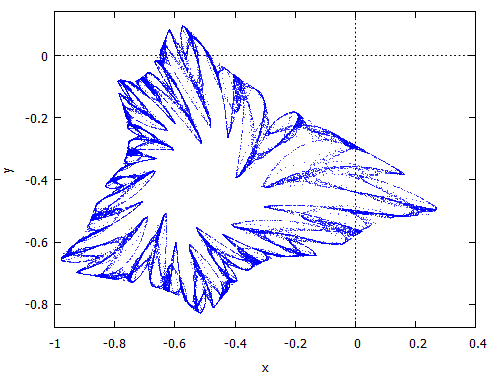
解説ページにある例は、見事にカオスでフラクタルな図形を描きます。
f: 0.6*x*(1+2*x)+0.8*y*(x-1)-y^2-0.9$ g: 0.1*x*(1-6*x+4*y)+0.1*y*(1+9*y)-0.4$ evolution2d([f,g], [x,y], [-0.5,0], 50000, [style,dots]);
解説ページにある上記例は、拡大するとフラクタルな雰囲気がありあり。
しかし上記のような図形を描く漸化式は簡単には見つかりませぬ。
試みに、非常にシンプルな「連立漸化式」を evolution2d に与えてみました。
a: 3*x+y$ b: 2*x+2*y$ evolution2d([a,b], [x,y], [2,-1], 10, [style,dots]);
そのプロット結果は以下に。最初の10個のつもりがドット間隔が粗すぎ。老眼の目に見えないので、赤で矢印してみましたぞ。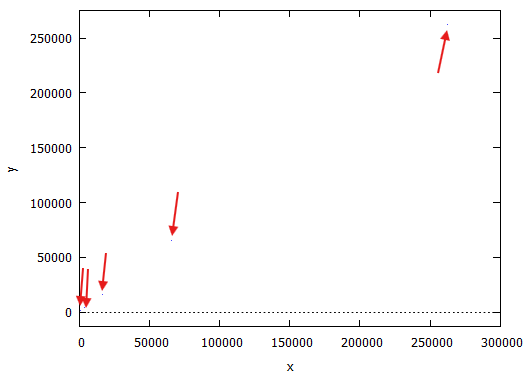
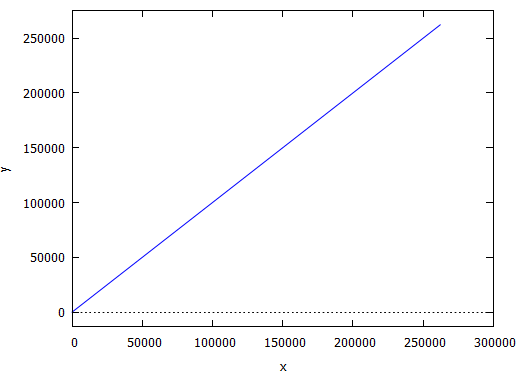
ドットではラチが空かないので、以下のようにして「線でつなぐ」形で書き直しました。
evolution2d([a,b], [x,y], [2,-1], 10, [style,lines]);
一直線じゃん!
なお、上記の「連立漸化式」については、いつもお世話になっております『高校数学の美しい物語』様の以下のページを参照させていただいております。
上記ページに胸に染み入るお言葉がありました。1行引用させていただきます。
連立漸化式を解くということは行列の n 乗を求めることに他なりません。
確かに。evolution2d関数の一面をも表しておると、いいのかそういうことで?