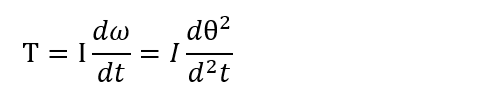前回までで「回転」を扱うための準備が出来た感じがします、気のせいかも知れないけど。そこで今回から「回して」いきたいと思います。まずは最も単純なケース、ブレない一本の軸の周りで剛体(形が変わったりしない)を回してみます。慣性モーメントの復習からだな。角加速度を2回積分すれば角度ってか。シミュレーションは簡単。
※「ブロックを積みながら」投稿順 index はこちら
※動作確認にはWindows 11の パソコン(64bit)上にインストールしたScilabの以下バージョンを使用しています。
Scilab 2024.0.0
剛体の回転運動、慣性モーメント (moment of inertia)
さあてお惚け老人が、ぐだぐだごたくを並べてもせんないので、Webで見つけた『KIT物理ナビゲーション』様のページへのリンクを貼り付けておきます。
「本気で」回転扱おうとすると、回転軸はどうなの?回転体の密度は変化するのでないの?形は?などと問題がいろいろでてきます。でも初回の今回は、
-
- 軸は一本、ブレたりしない
- 回るのは剛体、形は変わらない
- よって、回転軸周りの慣性モーメントはスカラー量として計算してよい
- 1個の外部トルク源でトルクを与える
Tはトルク[Nm]、Iは慣性モーメント[kgm2]、ωは角速度[rad/s]、θは回転角度(積算)[rad]です。
Xcosのフロー
今回フローが以下に。右半分は以前から使っていた回転をアニメーション表示するための仕組みです。前回「スーパブロック化」したのに元に戻っているのは今回のところは中身を分かり易くするためです。次回はスーパブロック化版に戻す予定です。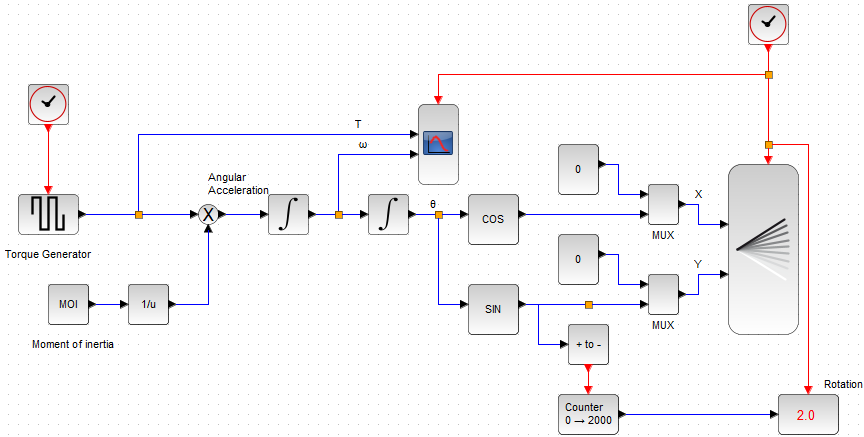
左半分が、上記のシンプルな回転の運動方程式を実装した部分です。トルクや回転モーメントなどの具体的な数字は、コンテキスト設定においてあります。こんな感じ。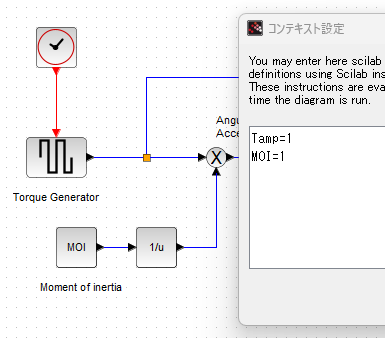
一方、シミュレーション・パラメータは以下のようです。シミュレーション時間は10秒、そして実時間スケール(アニメーション表示のスローモーションの倍率)は2倍です。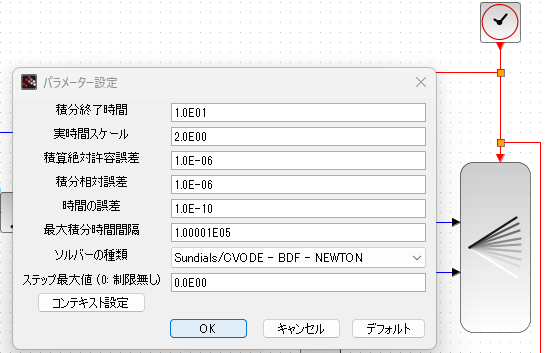
例によって、BARXYブロックのアニメーションは「単なる棒」ですが、2倍のスローモーションで棒がくるくる回ります。
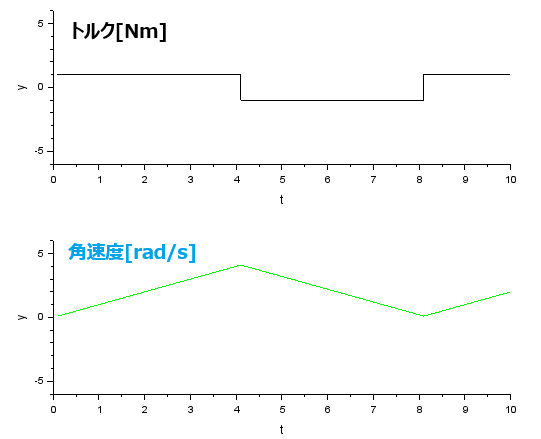
シミュレーション結果
一定のプラスのトルクで角速度が上昇、マイナスのトルクに変わると角速度が落ちていきます。そして再び加速。
このグラフの通り、アニメーションも最初緩やかな回転から速く回り、そして速度が落ち、再び加速と。動画は、あまりスペクタキュラーでもないので貼り付けませぬ。地味だわな。