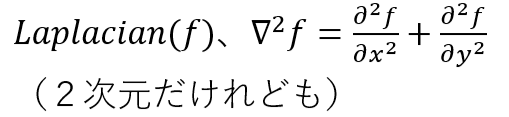grad、div、curl(rot)と練習してきて今回は Laplacian です。過去回はスカラー場からベクトルが飛び出てきたり、あるいはその逆であったりしました。今回は地味。スカラー場をLaplacianすると出てくるのはスカラー。でも計算の奥底にはベクトルが息づいている？凸とか凹とか調べるのにお馴染みの操作です。
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
毎度のvect パッケージ
過去回では「ベクトル場」をプロットするのに plotdf パッケージのお世話になってきましたが、今回のプロットはスカラーで地味なのでplotdfはお休みです。使用するのはベクトル解析用の vect パッケージのみ。以下にマニュアルページ（日本語）へのリンクを貼らせていただきます。
23. Matrices and Linear Algebra
Laplacian
画像のエッジを検出するときの「ラプラシアン・フィルタ」は定番です。といいつつ信号処理の別シリーズなど眺めていたら、他のフィルタは練習していたのに、肝心の「ラプラシアン・フィルタ」はやってませんでした。トホホ。
今回 Maxima様のvectパッケージの中で定義されているベクトル微分演算子群の一つ Laplacian は、３次元のスカラー場が凹になっていたり、凸になっている様子を計算できる演算子であります。しかし「３次元の場が凹になっている」様子などは、お惚け老人がよく描けるところにないです。例によって１次元を端折って、場は２次元、描画は３次元風で行きたいと思います。
２次元のときのラプラシアンが以下に。
プロット例
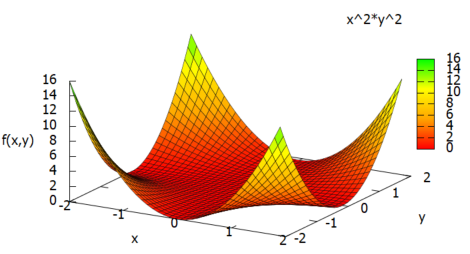
まずはラプラシアンを計算する対象のスカラー場を以下のように定義してみました。
f(x, y):= x^2 * y^2;
f(x, y)の値をz方向にとってグラフ化してみるのはこんな感じでよいですかね。
plot3d(f(x, y), [x, -2, 2], [y, -2, 2], [grid, 39, 39], [palette, [gradient, red, orange, yellow, green]], color_bar, [xtics, 1], [ytics, 1], [ztics, 2], [color_bar_tics, 2], [zlabel, "f(x,y)"])$
プロット結果は以下のようになります。
原点（０，０）に近いところでは平らかなのだけれども、原点を底として凹になっている「地形」であることが分かります。
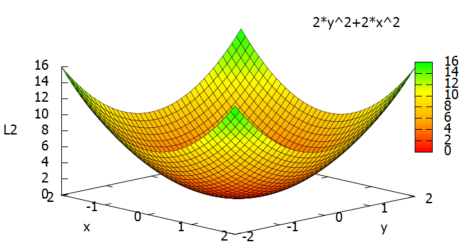
さて、vectパッケージを使って laplacianを計算し、その結果をプロットするステップが以下に。なお、vectパッケージはデフォルトで３次元を扱うようになっているので、dimension : 2 でことさらに２次元に抑えてくれるようにお願いしてます。
load ("vect");
dimension : 2;
L2: ev(express(laplacian(f(x, y))), diff);
plot3d(L2, [x, -2, 2], [y, -2, 2],
[grid, 39, 39],
[palette, [gradient, red, orange, yellow, green]],
color_bar, [xtics, 1], [ytics, 1], [ztics, 2],
[color_bar_tics, 2], [zlabel, "L2"])$
ラプラシアンの計算結果のプロットが以下に。
原点が底の凹ね。そんなの見れば分かるか。