このところvectパッケージのベクトル解析演算子共を試用。しかし、お惚け老人の「プロット能力の制約」により、その適用はいつも２次元空間でした。２次元のベクトル空間への演算子の適用結果を３次元プロットするのならば簡単。でも、本来３次元空間に対して適用するのが筋ってもんじゃありませんか。今回は少しジタバタしてみましたぞ。
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
今回試作の自前関数ども
Maxima様にはplot3d、draw3dなどの３次元プロット可能な関数が用意されております。どちらもお世話になっておりますが、今回は draw パッケージのdraw3dの方を使わせていただきました。日本語マニュアルページ（東北大様のサイト）が以下に。
あまりムツカシー方法は老人の頭がついていかないので、以下の方針としました。
-
- ３次元のベクトル場のプロットは、３次元空間内ｘ、ｙ、ｚの座標の「キリのいいところ」にその場所でのベクトルを矢印で描く。矢印の根本は「場所」矢印の大きさは計算したベクトルの値。
- ３次元のスカラー版のプロットは、３次元空間内ｘ、ｙ、ｚの座標の「キリのいいところ」に球体を描く。その場所のスカラー値を「色」で示す。
作製した自前関数は４つです。genVectsはベクトル場と計算領域を与えると描くべきベクトルのリスト（膨大になるかも）を返すもの。plotVect3dは、そのリストと描画領域を与えるとベクトルどもを矢印で描くもの。genPointsは、スカラー場の色付き球を置くべき点を計算してリスト（膨大になるかも）で返すもの。plotScalar3dは、そのポイントのリストとどのような色にするか「スカラー値」を与えて球体の並びを描くもの。なお、３次元空間の奥の方まで見えるようにするためには配置をスカスカにするのを推奨っす。
以下はMaxima用の関数定義のソース、何の芸もないです。forのネストで３次元回すというベタな形。
genVects(vecX, Lx, Ly, Lz) := block( [tL],
tL: [],
for i:Lx[1] thru Lx[2] step Lx[3] do (
for j:Ly[1] thru Ly[2] step Ly[3] do (
for k:Lz[1] thru Lz[2] step Lz[3] do (
tL: cons(vector([i, j, k],at(vecX, [x=i, y=j, z=k])), tL) ))),
tL )$
genPoints(Lx, Ly, Lz) := block( [tL],
tL: [],
for i:Lx[1] thru Lx[2] step Lx[3] do (
for j:Ly[1] thru Ly[2] step Ly[3] do (
for k:Lz[1] thru Lz[2] step Lz[3] do (
tL: cons([i, j, k],tL) ))),
tL )$
plotVect3d(dat, xr, yr, zr) := draw3d(
xrange=xr,yrange=yr,zrange=zr,
head_length=0.05, head_angle=10,proportional_axes = xyz,
wL)$
plotScalar3d(dat, sV) := draw3d(
point_type = filled_circle,
point_size = 2,
enhanced3d = [sV, x, y, z],
points(dat) )$
表示例
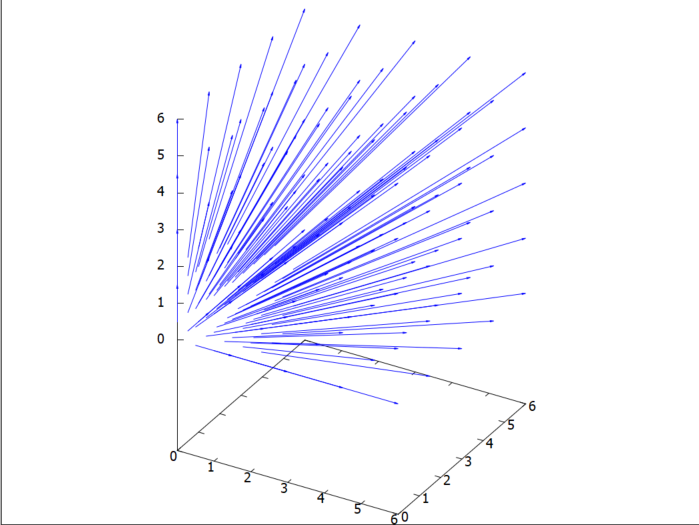
まずはベクトル場の表示例。計算にはお馴染み vect パッケージから、grad（勾配）関数を呼び出して「場」を計算してます。表示例のコードが以下に。
load ("vect");
v3: express(grad(x^2+y^2+z^2));
v3d: ev(v3, diff);
xlis: [0, 2, 0.5];
ylis: [0, 2, 0.5];
zlis: [0, 2, 0.5];
wL: genVects(v3d, xlis, ylis, zlis)$
plotVect3d(wL, [0,4], [0,4], [0,4])$
プロット結果が以下に。
つづいて、スカラー場の表示例。こちらで使っているのはdiv（ダイバージェンス）演算子です。
xlis: [0, 2, 0.25]; ylis: [0, 2, 0.25]; zlis: [0, 2, 0.25]; m: genPoints(xlis, ylis, zlis)$ E3 : [cos(x), cos(y), cos(z)]; V3: ev(express(div( E3 )), diff); plotScalar3d(m, V3)$
スゲー人為的な「場」なのだけれども、ダイバージェンスとった結果が以下に。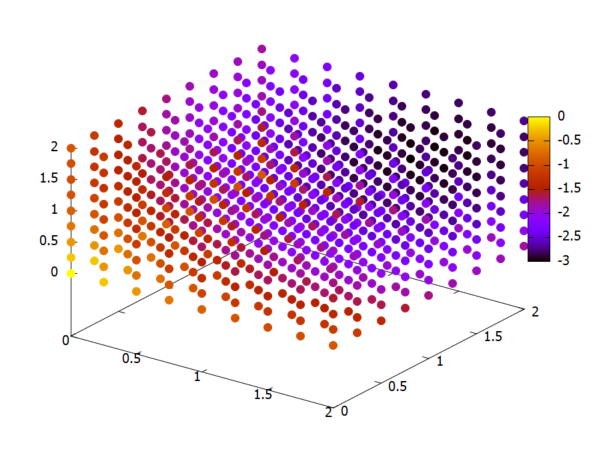
まあ、表示は出来ているみたい。結果が正しいかどうか知らんけど。いいのかそんなことで。