前回、3次元のベクトル場とスカラー場をお惚け老人なりにプロット。さて何か意味のあるものを描きて~ということになりました。そこで今回は、みんな知ってるクーロンの法則で描いてみたいと思います。想定は「原点に電子1個あり、その周りに別な電子1個を置いたときに働く力」です。まあ計算するまでもなく1点から周りにドヒャーと。
※「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
まあ上記想定は「場」というには問題ありーのな感じっすけど、まあ無理やりなプロット例に物理法則をホンワカ当てはめてみた感じっす。
クーロンの法則
泣く子も黙る(黙らないか)、クーロンの法則が以下に。
いわゆる逆2乗則ってやつ?知らんけど。これが計算できれば重力でもなんでも以下同文だと。ホントか?
今回は、原点にq0をおいて、その周りのどこかに別なq1を置いたとしたらそれにかかる力Fを、各場所毎にプロットしようという目論見です。だいたい、電子は停止していることないし、意味なしな計算?だけれども、ベクトルFは計算できるし、プロットもできると。
なおFがプラスなら斥力、マイナスだったら引力ってことで良かったハズ。
今回試作の自前関数ども
今回は前回試作の自前関数を流用してますが、早速バグ見つけて修正してます(plotVect3d関数。)
genPoints(Lx, Ly, Lz) := block( [tL],
tL: [],
for i:Lx[1] thru Lx[2] step Lx[3] do (
for j:Ly[1] thru Ly[2] step Ly[3] do (
for k:Lz[1] thru Lz[2] step Lz[3] do (
tL: cons([i, j, k],tL) ))),
tL )$
plotVect3d(dat, xr, yr, zr) := draw3d(
xrange=xr,yrange=yr,zrange=zr,
head_length=0.05, head_angle=10,proportional_axes = xyz,
dat)$
CoulombF(q0, q1, vR) := block( [k],
k: 9e9,
k * q0 * q1 / (vR[1]^2 + vR[2]^2 + vR[3]^2))$
Elec: -1.6e-19;
Dist: 5.3e-11;
Fcoulomb(v) := CoulombF(Elec, Elec, v);
Vcoulomb(v) := block ( [sV, fV, tV, xS, yS, zS],
sV: v * Dist,
fV: Fcoulomb(sV),
tV: SMax * fV / sqrt(sV[1]^2+sV[2]^2+sV[3]^2),
xS: sV[1] * tV,
yS: sV[2] * tV,
zS: sV[3] * tV,
vector([v[1],v[2],v[3]],[xS, yS, zS])
)$
真ん中辺に、ElecとDistという変数を定義してますが、Elecは電子の電荷[C]、Distは電子と原子核の間のほんわかした距離[m]であります。
表示例
以下の想定であります。
-
- 原点(0, 0, 0) に電子1個分の「電荷」-1.6e-19 [C]が存在する(固定!)
- 格子の距離「1」は原子核と電子間の「ホンワカした距離」5.3e-11mである。
- 格子の各点(表示例ではx,y,zとも 0.5づつ)、に別な電子1個が存在したときにその電子に働く力クーロン力F[N]を3次元ベクトル表示する。
まずは「格子」の定義より、ここで前回試作のgenPoints()関数を流用してますが、キモは原点(0, 0, 0)を格子から取り除くところであります。
xr: [-1, 1, 0.5]$ yr: [-1, 1, 0.5]$ zr: [-1, 1, 0.5]$ pr: [-1.25, 1.25]$ plist0: genPoints(xr, yr, zr)$ plist1: sublist(plist0, lambda([v], v[1]^2+v[2]^2+v[3]^2 > 0))$
取り除かないと、後で分母に0が現れて無限大(特異点モドキか?)が現れてしまいます。
矢印表示のサイジングのために以下の脇道計算を行って、最大の矢印長さを決めておきます。
CoulombF(Elec, Elec, [Dist, 0, 0]); xMin: [0.5, 0, 0]*Dist; FMax: Fcoulomb(xMin); SMax: 0.25 / FMax;
上記の格子の定義から、最大の矢印は距離0.5格子(最短距離xMin)のところにあることがお惚け老人にも分かります。そこでのクーロン力FMaxを求め、FMaxのときに矢印長さが0.25格子になるようにSMaxを計算してます。なお、各格子点のベクトルを計算する Vcoulomb関数は内部で大域変数DistとSMaxを参照している(手抜きだよ)のでここで定義しておかないと思うようなグラフになりません。
ここまで準備ができたら、格子点のリスト plist1 にVcoulomb関数を適用すれば各点でのベクトルが得られます。これをplotVect3dすればグラフになるっと。
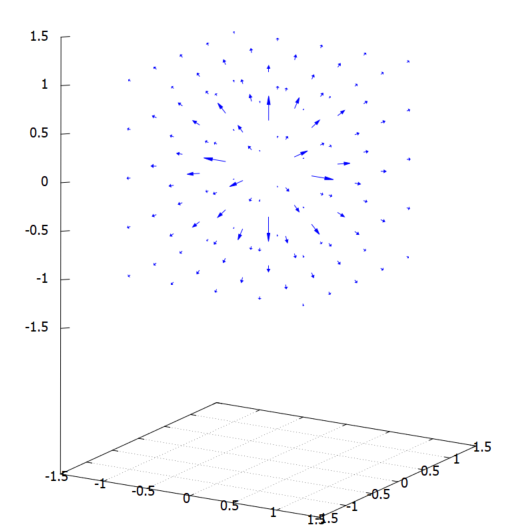
vL: map(Vcoulomb, plist1)$ plotVect3d(vL, pr, pr, pr);
こんな感じか?いいのかこんなもんで。