前回は指数関数。となれば今回は対数関数の練習必須でしょう。対数関数といってもその底はいろいろアリーノですが、日々お世話になっているのは常用対数（底は10、電卓ではLOG）と自然対数（底はeネイピア数、電卓ではLN）の２通り、あと計算機用に底２の対数計算できれば完璧かと。というわけで、今回も底の変換公式登場。
※「ぐだぐだ低レベル プログラミング」投稿順indexはこちら
※実機動作確認（といってもエミュレータなんだけれども）には以下を使用させていただいております。
FYL2XとFYL2CP1
前回の指数関数では１命令しかない命令と「指数関数の底の変換」公式と定数を駆使して計算するスタイルでした。今回の対数関数でも同じスタイルなのですが、命令は２つあります。
-
- FYL2X
- FYL2XP1
どちらも、スタックトップST(0)に引数Ｘ、ST(1)に引数Ｙを置いて
-
- Y * log_2(X)
- Y * log_2(X+1)
を計算する命令です。なお、ここで、引数範囲は以下のように制限されてます。
-
- x:ST(0)、 0 < x <∞
- y:ST(1)、 -∞ < y <+∞
This instruction provides improved accuracy over FYL2X when computing the log of a number very close to 1, for example 1 + ε where ε << 1.
なお、８０８７のマニュアルからするとFYL2XP1命令の方が若干クロック数が少ないデス。じゃ、FYL2XP1だけでもいいじゃん。でもまあ、引数にわざわざ1.0足すというのがメンドイ？
以下に、変換公式を忘れている「よゐこ」のために対数関数の底の変換公式を掲げます。
\( log_a b = \frac {log_c b} {log_c a} \)
上記は高校（中学？）で出てくるスタイルですが、８０８７用に使う場合は以下のような形で利用します。
\( y = log_n 2\)
\( log_n x = y log_2 x \)
なお、常用対数を求めたい場合は、yにlog_10(2)、自然対数を求めたい場合は、yにlog_e(2)を定数として与えます。8087は以下の定数ロード命令でこれを行えます。
-
- FLDLG2、 log_10(2)
- FLDLN2、 log_e(2)
その後で、FYL2X命令を実行すれば、常用対数なり自然対数なりが計算できるというもの。
今回実験のプログラム
今回の練習はFYL2Xの方を使って、100.1という一つの浮動小数値を常用対数、自然対数で求めてみます。
-
- log_10(100.1)=2.000434077479318640668921387778
- log_e(100.1)=4.6061696863211749012027923082893
例によって上記はWindows付属の関数電卓で計算した結果です。
なお以下は「強力なx86用アセンブラNASM」用のソースです（MSのMASMともインテルASM86とも微妙に異なるけど、まあ分かるっしょ。）
%use fp
segment code
..start:
mov ax, data
mov ds, ax
mov ax, stack
mov ss, ax
mov sp, stacktop
test:
; log_10 [src1 = 100.1]
fldlg2
mov bx, src1
fld dword [bx]
fyl2x
; e^[src1 = 100.1]
fldln2
mov bx, src1
fld dword [bx]
fyl2x
fin:
mov ax, 0x4c00
int 0x21
resb 2048
segment data align=16
resb 1024 * 63
src1: dd 100.1
segment stack class=STACK align=16
resb 2048
stacktop:
dw 1024 dup (0)
stackend:
アセンブルして実行
MS-DOS互換で機能強化されているフリーなFreeDOS上、以下のステップで上記のアセンブラソース flog.asm から実行可能なオブジェクトファイルを生成して実行することができます(nasmとwatcom Cがインストール済であること。）
なお、FreeDOS付属の「debugx」デバッガは、8087のレジスタ内容を浮動小数で見せてくれます。
nasm -f obj -l flog.lst flog.asm wlink name flog.exe format dos file flog.obj debugx flog.exe
まずはプログラムの逆アセンブルリスト。
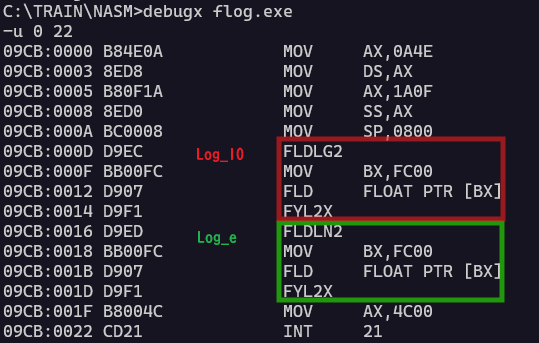
まずは常用対数をもとめるための準備部分。以下、赤枠のFLDLG2命令で赤枠のST1の定数（log_10 2)を、黄色枠のメモリロード命令で黄色枠の100.1相当の浮動小数値をロードしてます。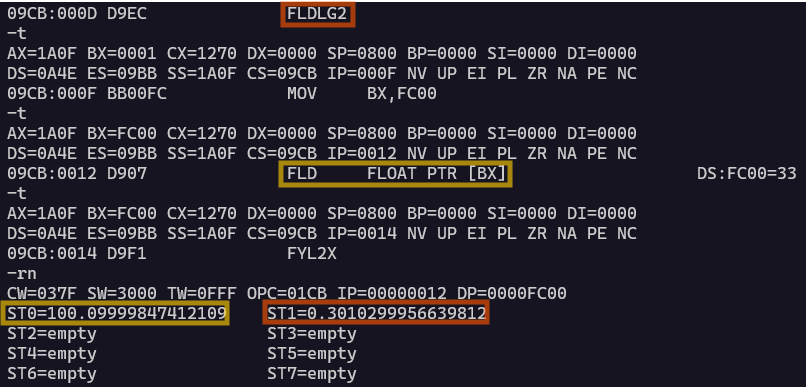
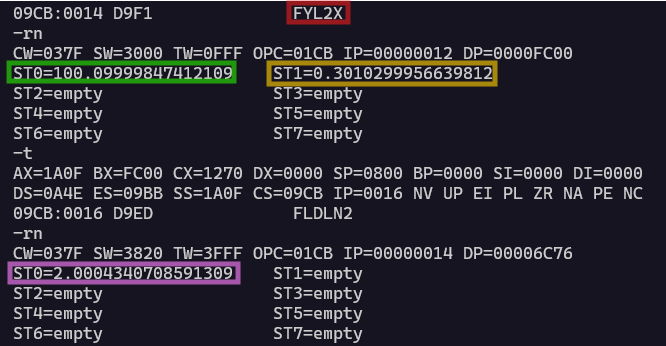
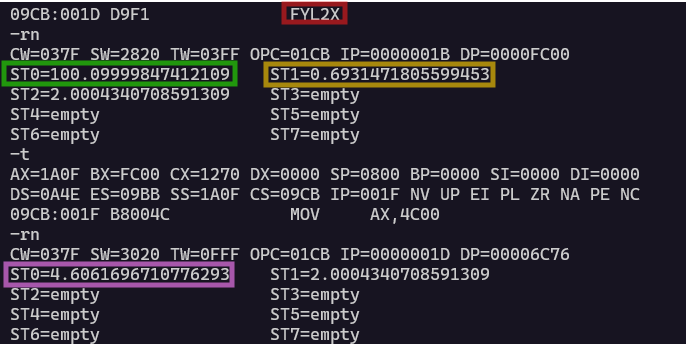
常用対数をもとめた結果が以下に。
黄色枠のY(ST1)と、緑枠のX(ST0)から、ピンク枠のお答えが求まってます。事前に計算した結果とほぼほぼ同じね。微妙？
さて以下では自然対数を求めてます。
こっちもOK（だいたい。）自然対数でも常用対数でもかかってこいと、お調子モンだな。