信号処理素人老人がScilabの「信号処理のデモ」からカテゴリ脱出。前回はDAE（微分代数評定式）で記述された「球面振り子」の動きに目を回しました。今回もDAEです。支点が曲線上を移動する振り子です。原題のまま「スライディング」と書くと別なものがヒットしそう。デモは支点がスライドするだけで制御はしてないんだが。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。（Scilabについては御本家 Scilab 様へ）
Sliding pendulum
今回のデモは、Scilabデモの選択画面の４階層目に隠されてます。そのカテゴリ Sliding pendulumとな。
そこには２種のデモがあり、今回はその両方を撫でてみたいと思います。２種のScilabスクリプトの在処は以下のパスです。
Scilabのインストールパス\modules\differential_equations\demos\dae\dae2
２種のデモとも、似たDAEで記述されとります。違いは支点の移動を拘束している曲線の形です。
-
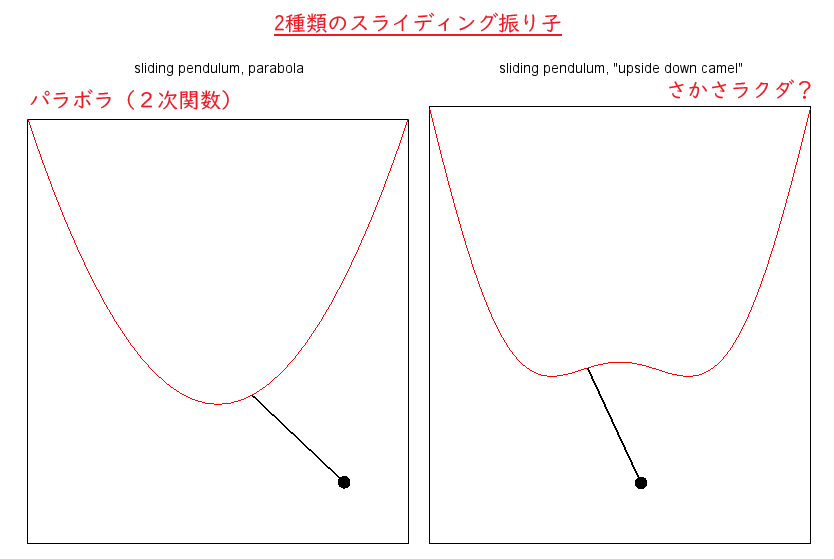
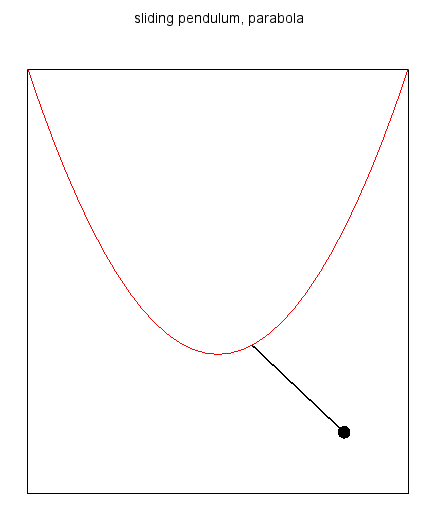
- 支点がパラボラ曲線（２次曲線）上を動くもの：pendg1.dem.sce
- 支点が「さかさラクダ」曲線上を動くもの：pendg2.dem.sce
なお、ラクダはふたこぶラクダっす。呼び出されるスクリプトの最上層は上記のように異なりますが、内部で呼び出している関数の多くは同じディレクトリ内のファイル内で「シェア」されてます。
なお、タイトルは Sliding pendulum ですが、制御をしているわけではないので、スライディングモード制御とは違うと思います。知らんけど。まあ、でも数学は決して「遠くない」？ホントか？
その挙動のムツカシさ
例によってGoogleの生成AI、Gemini 2.5 Flash様に、 Sliding pendulum の挙動のムツカシさを語っていただきました。こんな感じ。
上記でご指摘いただいているように「複雑な動きを視覚化」してみたものが以下に。
シミュレーション結果
シミュレーション結果はアニメーション表示され、「見ていて飽きない複雑な動き」を見せるのです。でも以下の静止画のスナップショットはあまりスペクタキュラーではありませぬなあ。
-
- パラボラ曲線拘束の場合
-
- さかさラクダ曲線拘束の場合
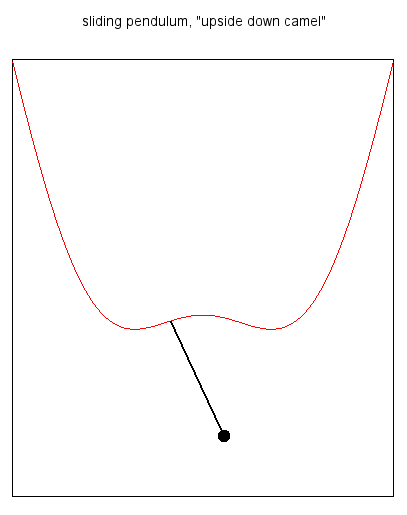確かに真面目にやったら物理の良いお勉強になりそうな課題っすけど、素人老人には気力も能力もなく、ただ口をあけてその挙動を眺めるのみ。