信号処理素人老人がScilabの「信号処理のデモ」からカテゴリ脱出。前回はついに泣く子も黙るソルバ「スイート」SUNDIALSに突入しました。その２回目の今回はローレンツ・アトラクタにArkodeソルバを適用するの回です。目にも止まらぬ？速さで6000点も処理してくれます。SUNDIALSの並列処理は強力。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。（Scilabについては御本家 Scilab 様へ）
ローレンツ・アトラクタ（ローレンツ・バタフライ）
「お手軽に」カオスが湧き出してくるローレンツ・アトラクタは、カオス業界？のハロー・ワールドです（誰が言った？）御多分にもれず本サイトの過去回でもなんどか「描いて」ます。
やっつけな日常(13) スマホでGo！じゃない。全てを引きこむローレンツアトラクタ
上記では、Go言語を使って描いてます。その時の方程式部分は以下のようでした。
dx = p * (y - x) dy = x * (r - z) - y dz = x * y - b * z
見直してみると、凄い単純な数値積分（上記にステップの固定時間幅を掛けただけ）を行ってました。また、その計算は１個の初期値に対してその軌跡を計算しているだけでした。
また、以下の過去回では、ScilabでもXcos(Scicos)のデモに収録されているものを鑑賞してます。
ブロックを積みながら(194) Scilab/Xcos、Xcosデモ、ローレンツ・バタフライ
上記の回では、方程式部分は以下のようでした。
-
- \(\frac {dX} {dt} = aY – aX\)
- \(\frac {dY} {dt} = -XZ + bX – Y\)
- \(\frac {dZ} {dt} = XY – cZ\)
さきほどの過去回で p、r、bと書いていたパラメータが、上記では a、ｂ、ｃとなってますが同じものですな。ここでもまた、計算は１個の初期値に対してその軌跡を計算してました。
SUNDIALS、Arkodeソルバ
さて、今回のSUNDIALSのデモの選択画面が以下に。
ソースコードの「方程式」部分を調べてみると以下のようです。
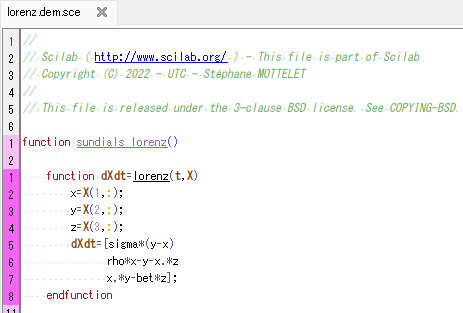
パラメータは sigma、rho、bet となってますが同じ形です。ただし、多数の点を含む配列を処理できるように定義されてるみたいです。
そしてこの方程式系を処理する部分が以下に。
ソルバは arkode だそうな。そして、初期値として乱数であたえた６０００点を設定してます。
例によって Googleの生成AI、Gemini 2.5 Flash様に arkodeソルバについて教えていただいたものからの抜き書きが以下に。
Runge-Kutta法（お惚け老人も辛うじて分かるよ）だけれども、時間ステップが動的可変だと、カッコいいです。
さらにGemini様は何でもお見通しです、Arkodeソルバをローレンツ・アトラクタの計算に適用する場合についても教えてくれます。こんな感じ。
緑枠の中のパラメータ、まさに今回のデモのソースで使っている値と同じではないですか。
さて実行結果の画面（最終の静止画）が以下に。
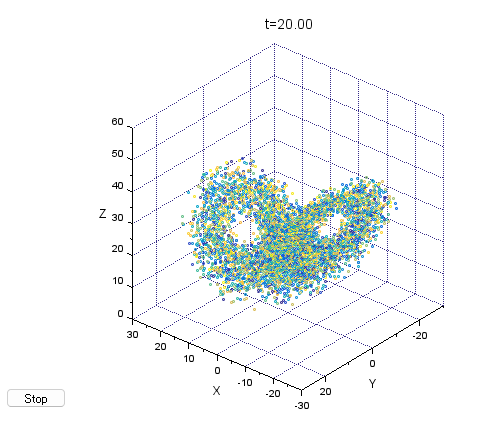
tの進行につれて、6000の点どもが、計算されまくって３次元空間の中でものすごいスピードで回転している様子が表示されます。お惚け老人は目が回るよ。SUNDIALS、流石デス。