
信号処理素人老人がScilabの「信号処理のデモ」からカテゴリ脱出。前回はSUNDIALSのcvodeソルバ使ったパラメータ推定でした。今回はidaソルバで解く「単振り子」です。単振り子、過去回で何度となく練習した記憶。なにをいまさらという感じもしないでもないです。しかし今更やるからにはそれなりみたい。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※Windows11上の Scilab2024.0.0を使用させていただいております。(Scilabについては御本家 Scilab 様へ)
SUNDIALS、Single pendulumデモ
さて、今回「鑑賞」してみるSUNDIALSのScilab呼び出しデモは Single pendulum です。そのデモンストレーション選択画面が以下に。
過去回で、もっとムツカシー振り子どもをやっているので、「なにをいまさら」感のあるテーマではあるのです。しかし、このアタリに登場するからには「それなり」な筈。
物理素人老人が、今回のデモスクリプトを眺めながらツラツラまとめてみたところではこんな感じかと。
-
- ありがちな単振り子のモデル化では、θ(角度)に対する1自由度の運動方程式を立ててそれを解くのが多い。するとシンプルな常微分方程式ODEのソルバで解ける。
- また、θは「微小角」だということで近似して解いてしまうことも多い(高校物理の定番?ホントか?)
- 一方、今回のモデリングでは、フツーのデカルト座標(x、y)使ってラグランジュ方程式を立てている
- その結果、x、y座標についての拘束条件(代数方程式)が必要になる
- よってODEでなくDAE(微分代数方程式)ソルバが必要になる
- また、粘性力(摩擦、空気抵抗など)のモデル(レイリーの散逸関数)も含んでいる
- ただし初期設定のままでは粘性力=0なので、振り子の振動は減衰しない
いつも何でもお見通しのGoogleの生成AI、Gemini 2.5 Flash様に「その辺の事情」についてお伺いしたときの様子が以下に。
さて、今回のデモスクリプトのファイル名は(いつものデモフォルダの中の)以下です。
demo_single_pendulum.sce
上記から呼び出される、実際の計算関数どもは以下のファイルに含まれております。
lagrangian_DAE.sce
そして実際に呼び出されているSUNDIALSのソルバは以下です。
ida
上記ソルバのHELPページが以下に。
SUNDIALS differential-algebraic equation solver
さて、デモのデフォルト値のままでシミュレーションを実行すると以下のような画面が現れ、60秒間、単振り子が振動(アニメーション)します。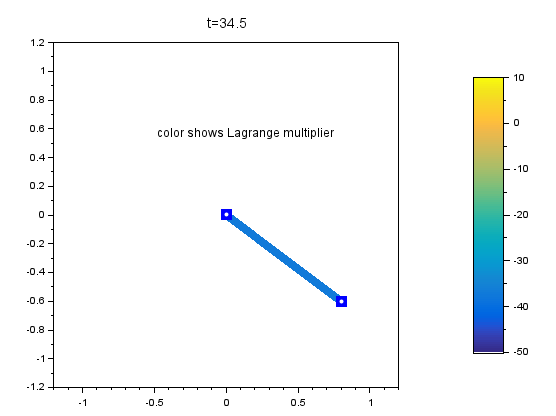
折角なので粘性力にテキトーな値を代入してみた
上記の初期設定のままだとずっと同じ振動が続くので面白くありません。デモ・スクリプトの冒頭近くに
function [Vd, Dd, Fd]=single_pend(t, x, u, mass, g)
という関数定義があり、その中に以下の行があります。
Dd = 0*u.';
どうもこの行が粘性力を計算する部分みたいです。デフォルト値は上記のように 0 がハードコードされてます。ここを 0.5 などとテキトーに非0の値に書き換えてやると振動が減衰するようになるみたい。0.5にしたら20秒くらいでほとんど振動しているのかしてないのか分からないくらいになりましたぜ。いい加減だな。