老「古老」介護にお疲れギミの数学素人老人デス。固陋な古老と付き合っているとこちらもヤラレてしまう恐れ多々あり。ただただMaxima様に御すがりして他力本願なんであります。拝読中の溝口純敏様著「Maxima を使った物理数学基礎演習ノート」（以下「演習ノート」と略）は今回「対角化」です。対角化したら良いことあるに違いなし
※ 「忘却の微分方程式」投稿順 index はこちら
※ MaximaおよびそのGUIであるwxMaximaの以下バージョンを使用させていただいております。
-
- wxMaxima 22.04.0
- Maxima 5.46.0(x86_64-w64-mingw32)
- SBCL 2.2.2 (SBCL = Steel Bank Common Lisp )
※Maxima を使った物理数学基礎演習ノート は以下のバージョンをダウンロードさせていただきました。
令和4 年3 月 第八回改訂
今回「演習ノート」を学ばせていただくのは、「4.2 行列とテンソル」の「4.2.10 対称行列の対角化」の前半あたりデス。
行列の対角化
何度となく練習した記憶が朧気な昨今であります。調べてみたら７回も練習してました「対角化」
(41) 反復練習５、対角化とｎ乗、Maxima on Android
(48) 反復練習１２、固有値と固有ベクトル、対角化 Maxima
(49) 反復練習１３、行列の対角化その２ Maxima
(52) 反復練習１６、対称行列Aを直交行列Uを用いて対角化、Maxima
(55) 反復練習１８、エルミート行列をユニタリ行列を用いて対角化
(56) 反復練習１９、エルミート行列の対角化の２回目、今度は３ｘ３サイズ
(150)反復練習１１３、行列対角化の応用、１階連立微分方程式、Maxima
こんだけ練習しても身に付いた気が全然しないのは、切実さが足りないのか、忘却力のせいなのか。。。
さて今回は、前回「テンソルの座標変換」の後の「対角化」です。「演習ノート」が「テンソル」を念頭に対角化をもってきたことは間違いないっす。
ここは 3.0 になったことだし、gemini先生に対角化についてお教えいただくことにいたしました。まずは対角化するとべき乗が求まる、ありがたや。
一方、線形変換、固有値やら固有ベクトルやらにも道は通じているみたい。
そうだったのねえ。
さて、それがテンソルに対してどうなのよ。
おっと、対角化で物理現象の本質に肉薄できるみたい。知らんけど。
いろいろあるでよ。おまとめが以下に。
確かに、テンソル、対角化してナンボだわ。
演習ノート
Maxima様に御すがりすればほぼほぼ一撃で対角化など出来てしまう筈なんでありますが、「演習ノート」では手順を追ってまずは「平手戦」にて対角化されてます。最初は
まず最初は、上記が正規行列であることを確認されてます。正規行列は「共役転置」して以下の関係がなりたつような行列らしいです。
\( A A^* = A^* A \)
Maximaで「共役転置」はadjointです。
正規行列でしたな。
さて、ここから「演習ノート」では固有値Λを求めに入ります。最初はこんな感じ。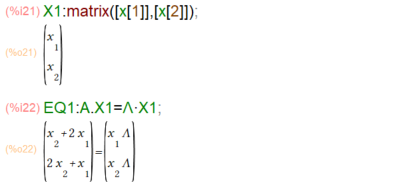
ここから以下のようになんやかんやあって、Λが求まります。
固有値Λが求まったら、固有ベクトルなど求めて、以下の対角化の結果へと計算を進めるみたい。
\( P^{-1} A P =
\begin{pmatrix}
3 & 0 \\
0 & 1 \\
\end{pmatrix}
\)
実際にMaxima様に御すがりしている様が以下に。
でも正直言うと、以下のMaxima所蔵の関数にお願いしてしまうのがお楽。
ここまでやっておいて、それかい？