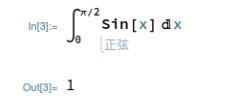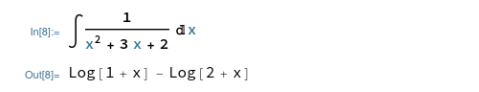前回は微分ということで、今回は積分です。わたしゃ自慢じゃないですが、積分が出来る気がしません。それもあってのMathematicaとMaximaに頼りたい症候群であります。今回は表面的なところを、おっかなびっくり、なでてみたいと思います。積分に関しては、Mathematicaの方が「分かり易い」感じ。何といっても入力の形からして。
※「忘却の微分方程式」投稿順 index はこちら
(MathematicaはRaspberry Pi3上の12.2.0.0、Maximaは、Windows 10上のwxMaxima 21.05.2(Maxima 5.45.1)を使用して動作を確かめています。)
このところ、毎度の進捗テーマは以下のWolfram社Mathematicaのチュートリアルに「準拠」させていただいております。
今回は分かり易い(個人の感想です)ということでMathematica先攻で行きたいと思います。
不定積分、定積分、数値積分
前回 Mathematicaの微分は D一文字だったですが、関数呼び出す場合はIntegrateと「ちゃんと」綴るみたいです。しかし、これには別な入力方法があり、
ESCキー押して、intt と打って、またESCキーを押す
と積分記号が現れます。なんかこれだけで積分出来てしまった雰囲気があります。□が出てくるのでその部分に所望の式や変数を書き込んでエイと、例によってシフトリターンすれば積分されます。きっと高校数学だと、不定積分をするときに積分定数をわすれるとシバカレルのかもしれませんが、MathematicaとMaximaもお構いなしです。
さてMathematicaの場合、不定積分にも独特の記法がありました。
ESCキー押して、dintt と打って、またESCキーを押す
今度は積分記号の上下にも□が現れ、定積分の範囲を記入することができます。以下の定積分の例では、sin(x)を定積分したので、数値で答えが出てしまいましたが、数値積分ではないので式で返ることもあります。
そして数値積分は、NIntegrateと頭にNをつけて、変数と積分範囲をリストで指定すればOKみたいです。Mathematicaのリストは例によって中カッコくくり。

さて、Maximaの方も積分は、integrate()です。ただし、例によってMaximaは小文字始まり(Mathematicaは大文字始まり)であります。
Mathematicaの場合は入力時点で、積分記号を使った入力ができましたが、Maximaの場合は、シングルクウォートしてやれば、積分記号を使った形での表示出力が可能です(出力です。)
不定積分だろうと定積分だろうと integrate()1つで出来ました。不定積分の場合は積分範囲を第3,第4引数に与えればOK。
しかし数値積分については、関数 romberg()を使わないとならんようです。ロンバーク積分。多分、Mathematicaも中で同じアルゴリズムを使っているのかもしれないですが(ホントかどうかは知りません)、Maximaは時々衣の下の鎧をさらけ出すことがままあり、ビビリます。
積分の検算
私には今や積分はほとんど不可能な領域になっておりますが、MaximaやMathematicaにとっても結句「ムズイ」相手ではあるようです。どうもそれらしい答えが出たからといって、鵜呑みにしてはいけないみたい。。。
以下の積分の検算をやってみました。まずは Mathematicaから。
最初は積分したところ。
 まずは、D[]で微分。微分した結果をToghether[]で通分。そして最後に分母をExpandAll[]で展開すれば元に戻りました。よかった。
まずは、D[]で微分。微分した結果をToghether[]で通分。そして最後に分母をExpandAll[]で展開すれば元に戻りました。よかった。
次は同じことをMaximaでやってみます。まずは積分から。
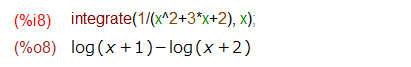 積分結果は、Mathematicaと同じ結果が得られましたな。
積分結果は、Mathematicaと同じ結果が得られましたな。
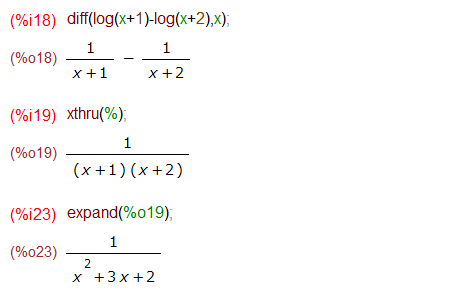 微分して(diff)、通分して(xthru)、展開(expand)と関数のお名前は違えど、ほぼほぼ同じ手順で「元に戻り」ました。よかった。
微分して(diff)、通分して(xthru)、展開(expand)と関数のお名前は違えど、ほぼほぼ同じ手順で「元に戻り」ました。よかった。