前回に引き続き今回も微分方程式です。今回は数値解の求め方について、Mathematicaの例題をMaximaでも解いてみた、という感じです。例によって、良いように勝手にやってくれるお楽なMathematicaと、ちゃんと自分でやれよ、という感じのMaximaという感じ。結構辛いよ素人には。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版)です。Mathematicaはラズパイ上の12.2.0.0です
※勝手に参照させていただいておりますWolfram社Mathematicaのチュートリアルは以下です。
今回は上記のチュートリアルに書かれている例題2つをやってみています。
例題その1
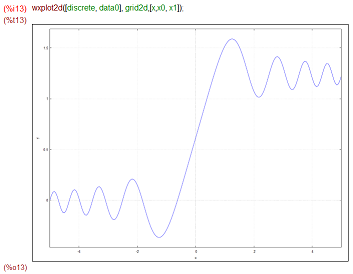
勝手に例題その1などと書きましたが、Mathematicaの例題は以下の通りです。1行で数値解が得られる上、結果は後で加工が楽そうなInterpolatingFunctionなどというものの中に入っています。Plotに渡すだけでグラフを描いてくれもします。ラクダ。
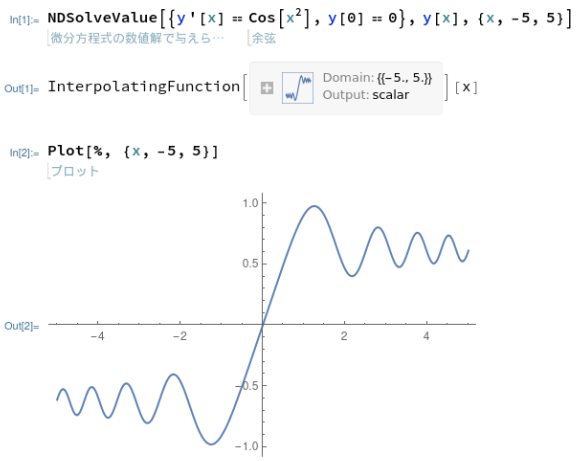
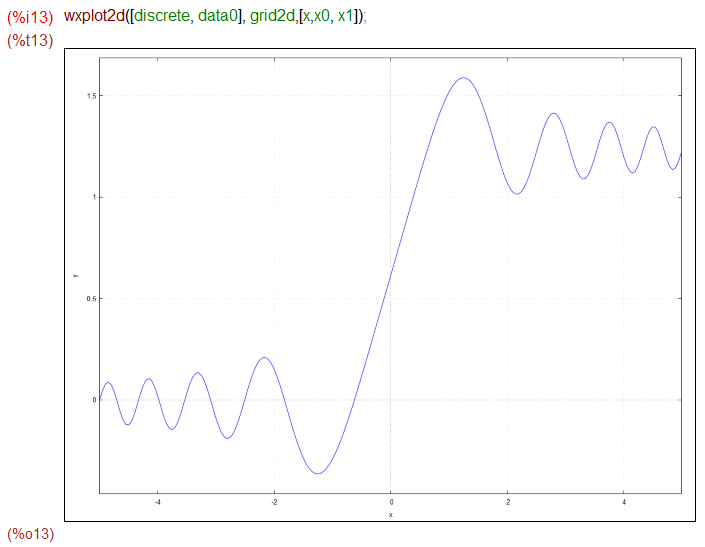
同じことをMaximaでやる場合、1行で書くのことも不可能ではありませんが、ステップ踏んで途中結果を残していった方が、後で修正が効くので楽そうです。
f1(y,x):=cos(x^2) x0: -5 x1: 5 N: 200 h: float((x1-x0)/N) data0: rk(f1(y,x), y,0,[x, x0, x1, h])
プロットに関しては discreteとか指定しないとダメだと思います。何も考えずには出来ないってことかい。でもま、ここはそれほど難しくはないです。
例題その2
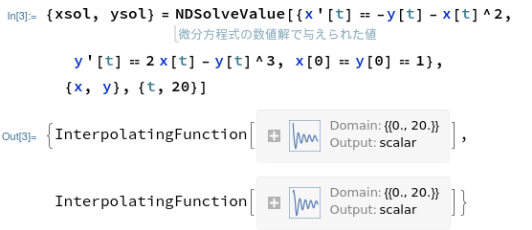
その2は、連立微分方程式ぞな。その上、パラメータtで媒介変数プロットせよと。Mathematicaの方は例題どおりなので、うちこむだけ。
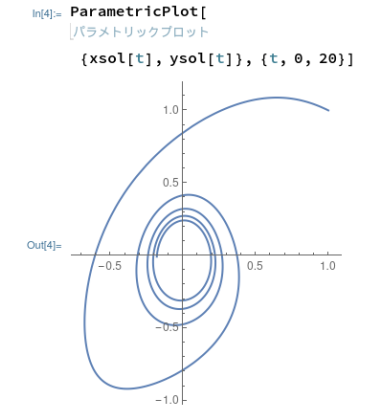
Maximaの方も出来上がってみれば大したことはなかったですが、以下の「表現」にいたるまで、結構苦労いたしましたぞ。やれば出来るのですが、知らないとどうして良いのか分からないことが多いです。
deq1: -y-x^2 deq2: 2*x-y^3 sol: rk([deq1, deq2],[x,y],[1, 1],[t,0,20, 0.02]) xylis: makelist([c[2],c[3]],c, sol)
お答えの中から makelist で t を滅して x, y だけにすれば parametric 指定しなくとも普通に plot2d で描けます。というか、parametric plotに descreteの結果を渡すことができるのか?分かりません。
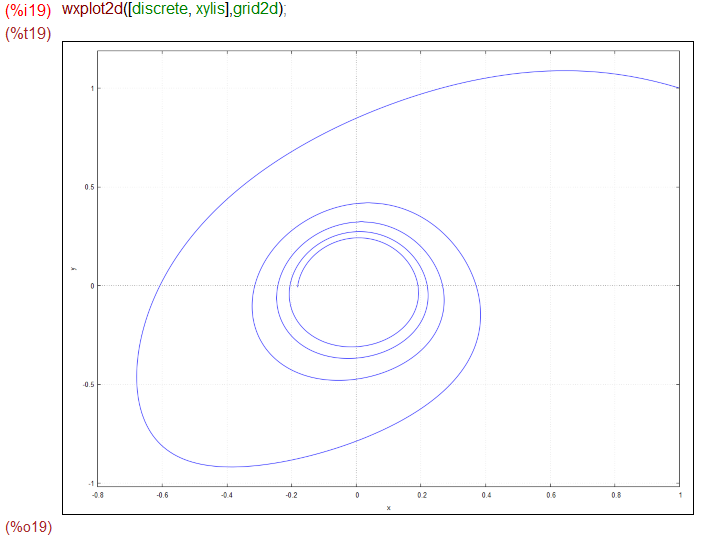
まあ、良く分からないのだけれど、同じようなグラフが描けたので、まずは一件落着。しかし凡人は相当練習しないと実用にならんぞ、これは。