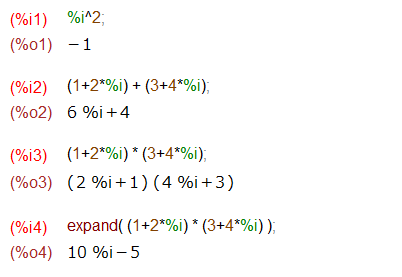微分方程式にじっくり取り組む前にひとまず一通り学ぶべく、さっさと先に進めることにいたしました。今回は複素数の取扱いについてです。基本のキなのでMathematicaでもMaximaでも同様な機能は備えていました。しかし両者の「御家流」は大分違うようです。さっさと「一通り」やった後、再び微分方程式に戻ってくる予定。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版)です。Mathematicaはラズパイ上の12.2.0.0です
※学生でもないのに勝手に参照させていただいておりますWolfram社Mathematicaのチュートリアルは以下です。
虚数、複素数の表記と加算、乗算
Maximaの場合、虚数 i を表記する場合、%i です。
上記のように、2乗すれば-1が返ります。複素数は %i を使って a + b * %i というスタイルで書けます。複素数の足し算自体は、即座に評価されて結果が返ってきましたが、複素数の掛け算については、手元の環境のデフォルト設定では、即座に評価してくれませんでした。expand() 関数に掛け算の式を渡せば評価してくれます。
Mathematicaの場合、他の定数などと同様大文字一文字で I (アイ)と書けば虚数となります。またMathematica特有の記法、CTRL+6 を使えばべき乗もカッコよく書けるので、以下のように書けます(小文字の i または、jになれているので大文字はちょっと抵抗ありますが。なお、j は電気系で使われる記法です。i は電流と間違い易いからと、昔から言われておるような。)
Mathematicaの場合、複素数の足し算だけでなく、掛け算でも即座に評価してくれます。Mathematicaでは、*記号を書かずとも数学式に掛け算が書けるので、見た目が良いです、そのかわりタマにハマります(個人の感想です。)
三角関数、指数関数
電気電子系であると複素数を使う理由の大半がここですな。
まずMaximaの場合です。三角関数に複素数を与えたときの展開。普通のexpand()関数では展開してくれず、三角関数用のtrigexpand()関数に与えると、展開してくれます。
次に指数関数表記から三角関数へは rectform()関数で変換可能でした。逆に三角関数表記から指数関数表記へはpolarform()関数です。ただし、手元の環境でpolarform()使うとかなり見苦しい結果がまず返ってきます。その結果をtrigsimp()に渡すとルートのところは簡略化してくれましたが atan2の角度のところは処置してくれませんでした。どうしたら良いの?現状、不明。
一方、Mathematicaの方は、かなり分かり易いです。どれも関数一発で変換可能。ただ1点つまずいたのは、最初の行の b I の部分です。b I とスペースを空けて入力すれば b かける I(虚数単位)と理解してくれるのですが、bIとスペースを空けないと単なる変数名 bI です。数字とIは続けて書いても掛け算と認識されるので、ついついそれに慣れて手が滑ると良く分からない結果が戻ってきます。掛け算のときはスペースあける習慣をつけた方が無難。
共役、実部、虚部、絶対値、偏角
Maximaの場合は、「小分け」にひとつづつ関数があるので、それぞれの関数に複素数を渡してやれば、所望の結果が返ります。こんな感じ。
一方、Mathematicaの場合、共役を意味するらしいグリグリ印?を入力するのは例によって ESCキー co ESCキーというシーケンスです。
実部虚部は ReIm[]関数で、絶対値と偏角は AbsArg[]関数がリストで返してきます。その方がタイプする量少なくて済むか?
ガウス平面のプロット
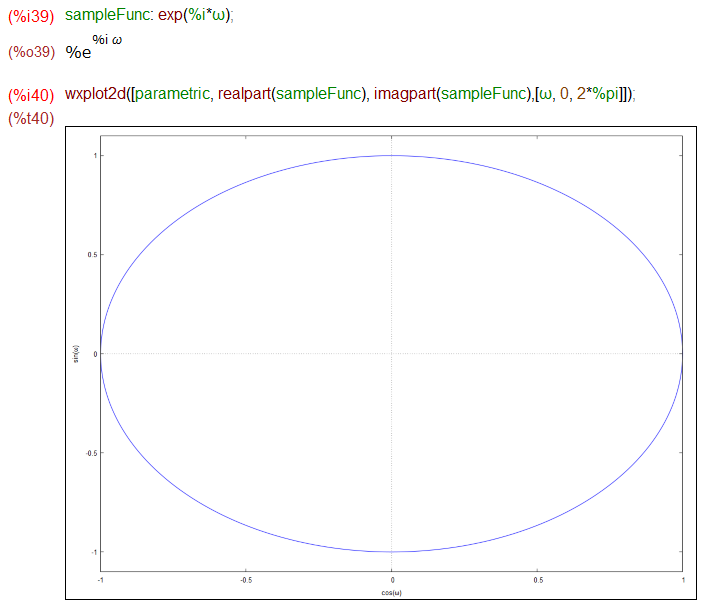
Maximaで、指数関数表記の単位円をパラメトリック・プロットしたものが以下に。xに実部、yに虚部を与えて、パラメータωで媒介変数表示させる、と。
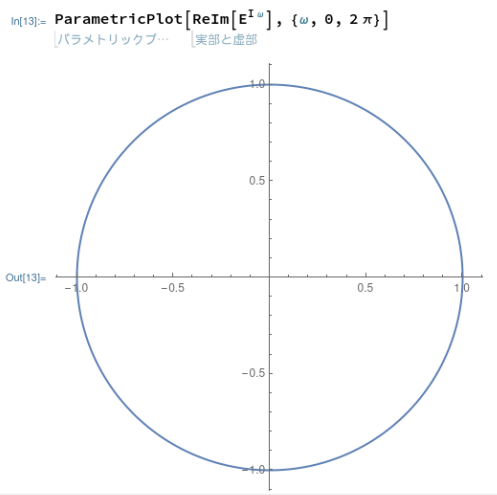
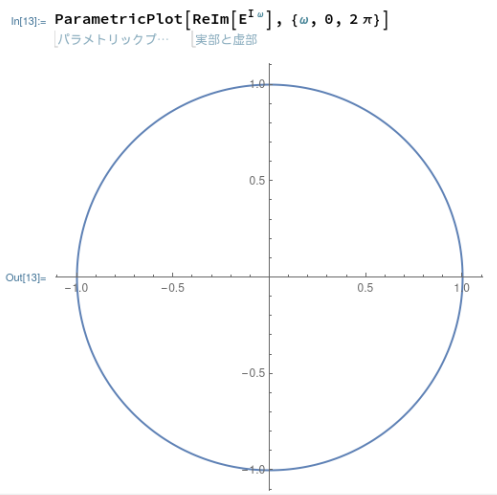
一方、Mathematicaで同じことは、そのものズバリのParametricPlot関数にお願い。例によって、ネイピア数(自然対数の底)が大文字のEなのは見慣れぬ目には抵抗があり。そのうち慣れるか。慣れてきたような気がします。それにしてもMathematicaは最初から画面の縦横比を考えて描画してくれるので美しい円です。
オマケに、Maximaで極座標で2次元プロットしたものがこちらに。polar()関数をplotに渡せば描いてくれましたが、デフォルトのままだと「カクカク」の見苦しい円になります。どうも parametric指定のときとは分割の塩梅が違うみたいです。nticks=を適当に大きくすると細かく分割して滑らかな円になりました。こんな感じ。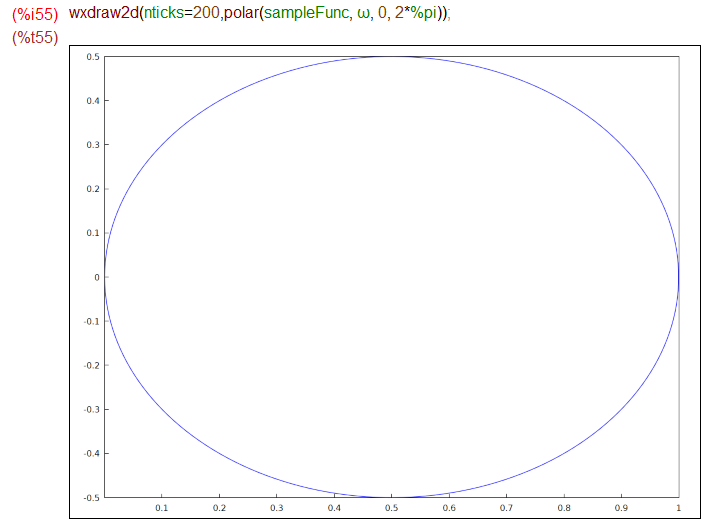
大体、複素数(といっても表記の仕方だけだったですが)はいいかな。どんどん先へ進めましょ。