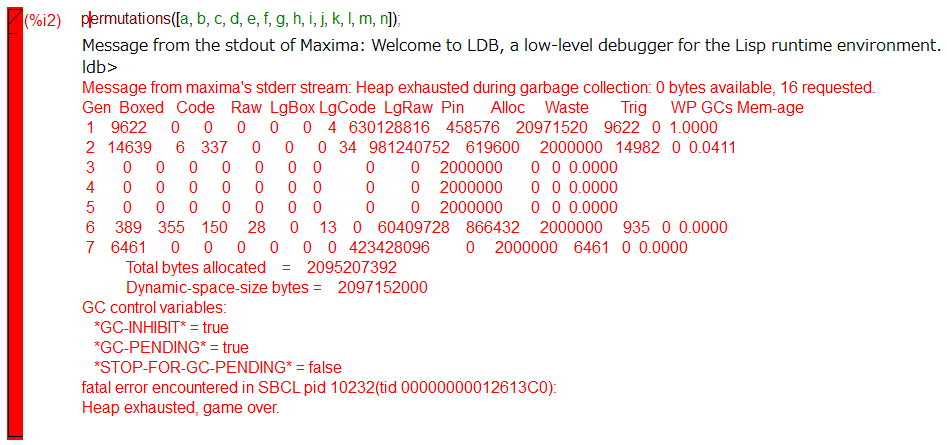
今回は深みに入らぬように気をつけていたつもりでしたが、Maxima様からきついエラーメッセージいただきました。”game over” とな(詳細は冒頭のアイキャッチ画像ご覧ください。)調子こいているんじゃねえ、という感じでしょうか。やっていることは簡単そうですが、気をつけないとヤバいです。
※「忘却の微分方程式」投稿順 index はこちら
※文中で Maximaとあるのは、MaximaにGUIを被せたwxMaxima 21.05.2 (Windows版)です。Mathematicaはラズパイ上の12.2.0.0です
※学生でもないのに勝手に参照させていただいておりますWolfram社Mathematicaのチュートリアルは以下です。
最初は素因数分解から
Maximaの場合、factor()関数に式でなく、整数を与えると素因数に分解してくれます。また、ifactors()関数に整数を与えると、素因数とべき乗のペアの形のリストで返してくれます。
一方、MathematicaでもFactor[]関数に整数を渡してみると、以下のようにすげないです。FactorInteger[]関数という素因数を求めるための関数は別にありました。そちらを使うとMaximaの ifactors()関数同等のリストが返ります(例によってMaximaは大カッコ(角カッコ)、Mathematicaは中カッコというお作法の違いがありますが。)
なお、MathematicaのFactor[]関数に式を与えれば上記のように因数分解してくれます。
最大公約数、最小公倍数
珍しく、ここは両者の意見が一致(違える方が難しいか)、関数は同名です。ただし例によってmaximaは小文字、Mathematicaは大文字。まずMaxima。
次にMathematicaの場合。
そろそろヤバそうな雰囲気、素数関係
素数関係は、似たような機能がありつつも、それぞれ独自の道を行っている感じ?両者ともにクセが強そう。
まずはMaxima、「素数ですか?」と聞く関数は primep()と。末尾のpはもろ Lisp的な雰囲気がありあり。lisp(common lisp)の人はなんちゃらピー?って言いがち?
totient()関数は、引数 n と互いに素であるような n 以下の整数の数とな。数学素人の私には使い道がとんと分からないデス。
ある範囲の素数を列挙してくれるのが primes()関数。また、特定の整数より小さい最大の素数は prev_prime()、大きい最小の素数はnext_prime()とな。この辺のネーミングはMaximaにしたら素直?
一方、Mathematicaの素数か否か判定する関数は PrimeQ[]です。Pとは口が裂けても言いたくないのか?
素数そのものは Prime[]関数に何番目かを指定すれば返してくれます。まるで素数の詰まった配列のごとし。また、互いに素であるか否かを判定するCoprimeQ[]関数などもあり。
整数の割り算
ここは、MaximaもMathematicaも意見が一致。商を求めるのはquotient、剰余を求めるのはmod。どちらも / で割ると 分数になるのは、お約束どおり。浮動小数で求めたいときは変換関数を通せ、と。
まずはMaxima。
続いて、Mathematicaで同じことを。
順列、組み合わせ
小学校でやるんだっけ、中学校?などと思っていたらMaximaから御叱りをうけてしまいました。
まずは、Maxima。似た名前の関数が二つ。permutationは以下の例のごとく、n個からm個を取り出すときの順列を求めるもの。一方 permutationsはリストの中の集合要素の全ての順列を「集合」として返してくれるもの。組み合わせの方は、専用関数 combination()でも、一般的な binomial()関数でも同じように求まると。なお、! で階乗は求まるので、遥か昔に習った式通りで pemutation計算するのもあり。
Mathematicaの場合、Binomial[]関数で組み合わせは求まれど、Combination[]は見当たらず。分かり易いお名前が多いMathematicaですが、今回はMaximaに負けてる?また、Permutations[]関数はMaxima同様、リストの中の集合要素の全ての順列を「集合」として返してくれるもの。結局、階乗つかって、遥か昔に習った式通りで permutation計算いたしました。
調子に乗って組み合わせ爆発が起こるような引数をMaximaのpermutations()に与えてみたら冒頭のごとし。衣の下の Lisp デバッガが顔を出し、
Heap exhausted, game over.
と。すみません、私が悪うございました。