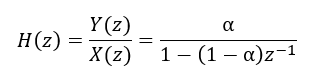Node-REDはIoTデバイスなどから集めて来たデータをWeb表示したりするときにとても便利なシステムです。昨日別投稿にてsmoothノードというものを勉強。入って来たデータの平均、最大といった統計量を求める他に、ローパス、ハイパスフィルタも含んでました。しかしHELPみてもフィルタ特性については書いてなかったです。
※ソフトな忘却力 投稿順 index はこちら
昨日の別投稿は以下です。
ブロックを積みながら(59) Node-RED、統計?信号処理?smoothノード
末端のデバイスから送られてきた生データを「ちょいと処理」するには良いものに見えるのです。確かにフィルタ掛けたくなる生データもあるし。しかし、フィルタの特性分からないと、フィルタ掛けづらいよね。ということでsmoothノードに実装されているフィルタ特性を「推定」してみました。
ソース読めば分かるでしょうが、メンドイです。昨日データをとった10点のデータがあるので、そこから「推定」してみようという暴挙であります。このごろ、別シリーズ「手習ひデジタル信号処理」で少しばかり信号処理を勉強しているので調子に乗った?ためです。大丈夫か、自分。「ソフトな忘却力」シリーズでは、Octaveを使わせていただくことが多いのですが、「手習ひ~」の方ではScilab使っているので、今回はScilabで行かせていただきます。
LPFの推定
smoothノードに実装されているフィルタは単純な差分方程式で計算できるような一種のIIRフィルタのようです。特性を決めるパラメータはN一つだけ。このNから計算できる係数1個を使ってLPFを構成しているみたいです。
N=5のときの10個のデータを眺めながら「推定(妄想)」した差分方程式が以下に。
y[n] = (1-α)*y[n-1] + α*x[n]
α=1/N
本当にこの方程式で smoothノードの出力と一致するかどうか確かめるために、昨日の結果と同じ結果が得られる「筈」のScilabコードを書いてみました。こんな感じ。
clc
clear()
N=5
alpha=1/N
x=1:10
y=[]
yprev=1
for i=1:10;
y(i)=(1-alpha)*yprev + alpha*x(i)
yprev=y(i)
end
上記の実行結果が以下に。Node-REDの出力と一致しとります。
差分方程式がOKそうなので、差分方程式から伝達関数を計算してみました。伝達関数の計算は、メモ用紙に手計算したのでイマイチ自信が無いです(中学生レベルの式の変形ですが、Maxima様かMathematica様にお願いした方が良かったか?)伝達関数(推定)が以下に。
伝達関数が分かれば、ScilabにBode線図を描いてもらうことができます。
// Node-RED smooth node LPF(estimated)
clc;
clear();
clf();
N=5
alpha=1/N
Hz = syslin('d', (alpha/(1-(1-alpha)*%z^(-1))))
bode(Hz, 0.01, 1.0)
xtitle("Node-RED smooth node LPF(estimated) 正規化周波数 Bode Plot(N=5)")
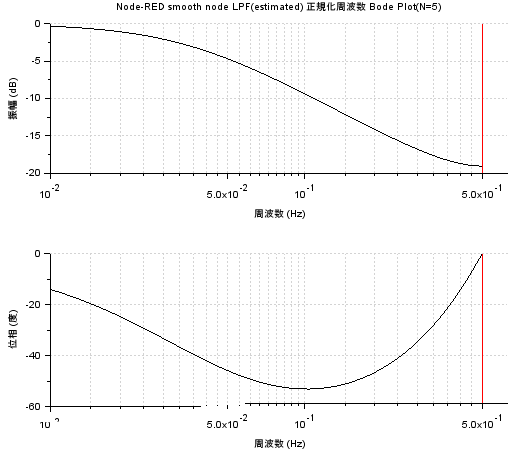
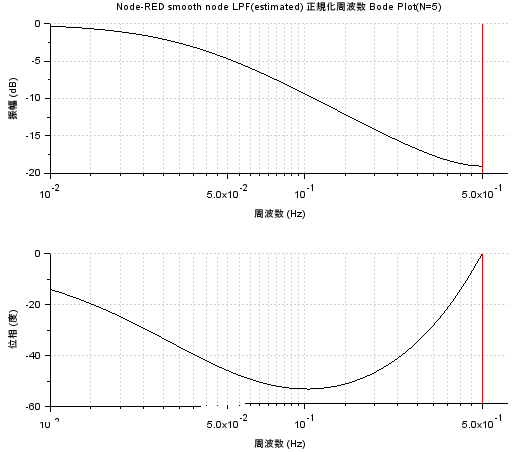
上記のコードで描いた「正規化」周波数対振幅、位相特性が以下に。デジタル・フィルタなので、サンプリング周波数を1Hzとし、ナイキスト周波数0.5Hzとした場合の特性です。
確かに、一応、ローパスしている感じはします。でも特性はダラダラなのね。N=5のせい?もっと大きくしたらスパッと落ちるのかね。
HPFの推定
それらしい結果がLPFで出たので、余勢をかって?HPFも求めてみます。まずはN=5の10点のNode-RED出力を眺めて差分方程式を妄想してみます。
y[n] = β*y[n-1] + β*(x[n]-x[n-1])
β=(1-1/N)
LPFの係数αとしたので、こちらはβとしてみました。上記の差分方程式でNode-REDと一致するのかどうかを確かめるためのScilabコードが以下に。
clc
clear()
N=5
beta=(1-1/N)
x=1:10
y=[]
yprev=0
xprev=1
for i=1:10;
y(i)=beta*yprev + beta*(x(i)-xprev)
yprev=y(i)
xprev=x(i)
end
上記のコードを実行した結果が以下に。Node-RED出力と一致しました。
差分方程式が決まれば、伝達関数が求まります(しかし、またもや中学生レベルの式の変形の手計算に自信が持てません。ぐだぐだ。)求めた結果が以下に。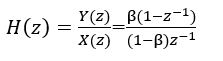
伝達関数が決まれば、Scilabのコードにするのは機械的。
// Node-RED smooth node HPF(estimated)
clc;
clear();
clf();
N=5
beta=(1-1/N)
Hz = syslin('d', ( beta*(1-%z^(-1)) /((1-beta)*%z^(-1))))
bode(Hz, 0.01, 1.0)
xtitle("Node-RED smooth node HPF(estimated) 正規化周波数 Bode Plot(N=5)")
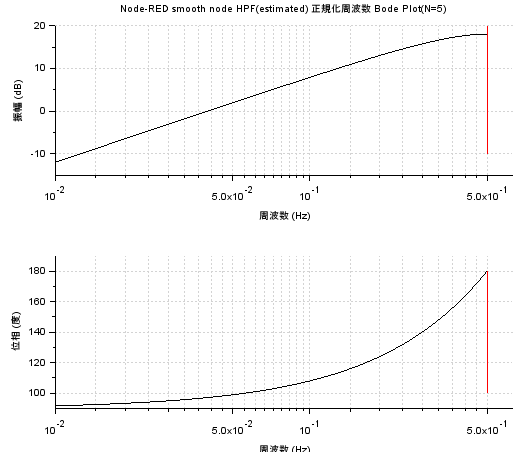
Scilabのコードがあれば、「正規化」周波数対振幅、位相特性は求まります。デジタル・フィルタなので、サンプリング周波数を1Hzとし、ナイキスト周波数0.5Hzとした場合の特性です。
まあ、ダラダラではあるけれど、ハイパスといえばハイパスな特性。やっぱりN=5のせいですかね。
まあ、本当はNをいろいろ変化させてシミジミ味わってみると良いのだけれど、今現在 smoothノードにお願いしたいデータも無いし。まあ特性求めるためのスクリプトの雛形は作ったので、smoothノードを使いたいときになったらやりますか(何時のことだか、自分。)