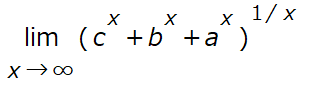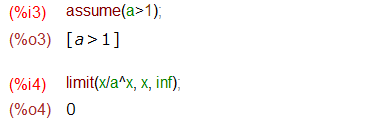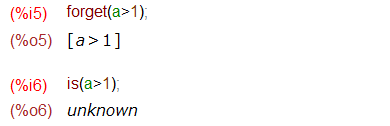今回も他力本願、Maxima様におすがりすれば、極限の計算のお答えをいただけます。しかし、今回はちょっと条件を指定しないと計算できない類の問題であります。そのときに活躍するのが assume とな。assumeすれば楽。でもassumeしているばかりでは後を引くので forget もせにゃならんと。能天気だな、自分。
※「忘却の微分方程式」投稿順 index はこちら
以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。不埒な。
予備校の先生がお書きになっている御本です。とっても分かり易いデス、といって数学の勉強になってないのだけれど。。。
今回はMaxima様が中に持つ「データベース」にアクセスをいたします。その辺のマニュアル(日本語)はこちらに。
条件を付けないと解けない奴ら
上記の教科書では「はさみうちの原理」のページに今回の問題が掲載されておるのです。直接求め難い奴らも上下から挟み込んでやれば極限を決定できると。しかし、Maxima様におすがりする場合にはただただlimitを求めてとお願いするだけです。問題はこんな感じ。
これをそのままMaxima様にお願いすると以下のようになります。何やら赤字でaに関する条件が正なんだか負なんだがゼロなんだかシツコク聞かれてしまいます。
テキトーにp(positive)と答えると、解答が求まりました。この問題、aの定義域によって「いろいろ」あるためだと思われます。無限大になったり、そもそも計算できなかったりするのでしょう。
上記をスッキリとくために登場したのが以下の assume です。assumeというのはMaxima内部の「述語論理」のデータベースに述語論理を追加するのだそうな。以下では a は 1より大きいよね、と宣言。すると上記のように聞かれることもなくすんなり極限が求まります。
なお、一度 assume するとなんやら「文脈」「コンテキスト」の中にいる限り有効である、と。文脈も枝分かれしたり切り替えたり、破壊されたりするみたいですが、その調べはまたそのうち。とりあえず、今いる文脈の中で特定の条件を「忘れる」ためには forgetすれば良いと。こんな感じ。
isを使えば、覚えているのだが、忘れているのだか確認できるようです。
勿論、再度 assume すれば記憶も復活。isで聞けば true を返してきます。「真」、「偽」以外に「知らない(unknown)」がある is 何気に凄い関数かも。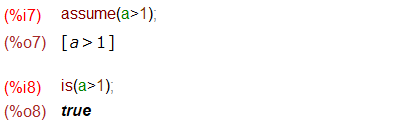
複数の条件をつけてみる
次の問題は結構メンドイです。a, b, c と3個も条件をつかなければならない定数?があり、その条件次第で答えが変わってきます。
以下は、3個の中で a が最大(a, b, cは全て>1)のとき。
assumeの中にズラズラと条件を列挙できました。このときのお答えはaだと。ということは b が最大なら b、cが最大なら c ってことですね。教科書では max(a, b, c)みたいなカッコイイ解答(当然手計算で)が書かれてましたが、maximaにそういうモノを求めるのは相当テクがいりそう?知らんけど。