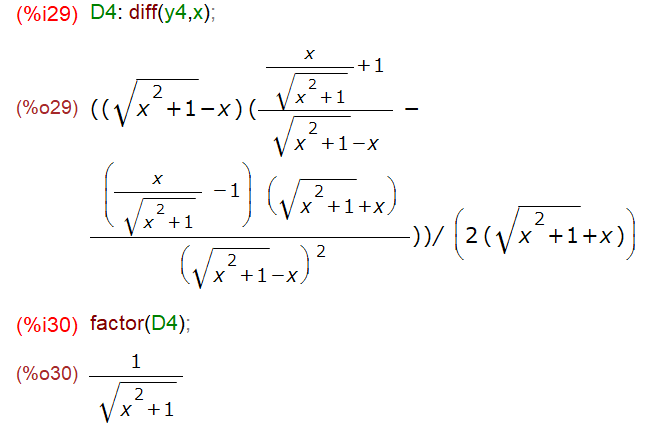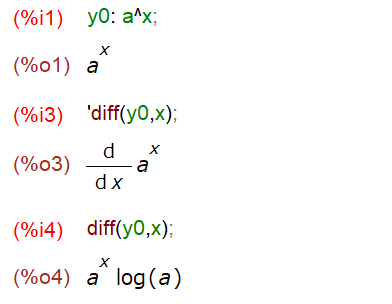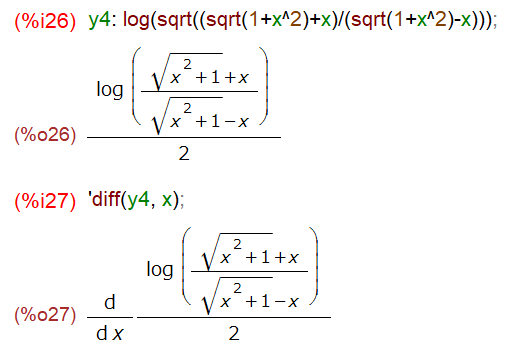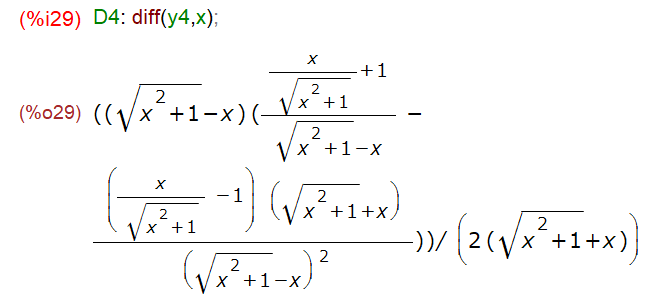前回から微分の練習に入りました。微分は「機械的に」解ける、ことが多いのでただただMaxima様におすがりすれば他力本願、「答え」はでます。でも前回みたとおりでそのままの結果では人間的にはイマイチ。前回は三角関数を含むものまでだったので、今回は指数関数、対数関数を含むものを練習しますです。
※「忘却の微分方程式」投稿順 index はこちら
数学のお勉強のための以下の教科書（参考書、問題集？）の例題をMaximaの練習に使わせていただいております。不埒な。
こういう御本がその昔にあったればよかったな。
まずは指数関数の微分
公式どおり。
続いて指数のところにCOSが載っているヤツ。合成関数の微分など考えなくてもMaxima様が良きように計らってくれまする。
続いて対数関数ありーの
対数関数の内側の絶対値のところ、入力時にabc()と書いても、ちゃんと絶対値記号にしてもらえるところが嬉しいデス。ただdiff()で微分しただけでは、ちょいと足らないです。結果が三角関数なので、trigreduce()すると「人間所望の形式」とあいなりました。
今度は対数関数の底がeでない、任意の値の場合です。とりあえず自前で「底の変換公式」用の関数を定義しておきました。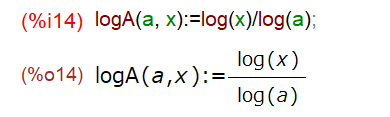
上記の関数を使うと問題はこんな感じに書けます。
微分はしていただけましたが、これはちょっと複雑だし、なんとかなるんじゃね？結局factor()、因数分解したらばよい感じになりました。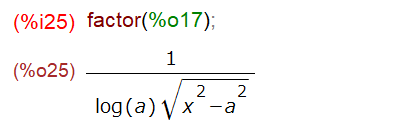
続いての問題はこんな感じ。結構複雑。
なお、以下のようにlog(sqrt(… とすると、シングルクォートしてもsqrt部分を1/2にしてlogの外側に括り出されてしまうようです。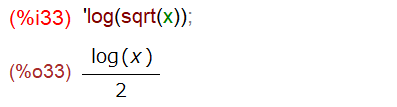 
さて、本題にもどってy4を微分してもらったものが以下に。いやあ、何言っているのか分からない。元の問題が複雑だから結果も複雑。
でもま、上記のような複雑な結果も、factor()で因数分解してしまえば、ほれこのように。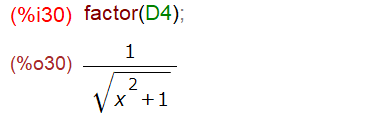
ここまで綺麗になると（まあ例題だから当然か。教科書のお陰。）カタルシス。