前回、前々回とScilab上で伝達関数から周波数応答を求めるのを練習していました。しかし、そういえば、ということで考えてみると差分方程式が与えられているのであれば、差分方程式から直接、時間応答が求まるのを練習してないじゃん、と。今回はそこんトコロを練習してみます。
※「手習ひデジタル信号処理」投稿順 Indexはこちら
※処理のターゲットは教科書の例題の1次のIIRフィルタです。伝達関数および、ブロック線図などはお手数ですが前々回をご覧ください。
さてターゲットの「1次のIIRフィルタ」の差分方程式
1次のIIRフィルタ、シンプル極まりないものであるので、差分方程式は以下です。DCでは入出力の振幅比が1である、という条件により係数b0とa1の間の条件も決まっております。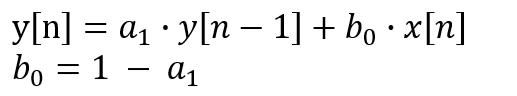
差分方程式への入力信号を定義する
過去記事で作成済の正弦波を生成する関数、周波数プロットをおこなう関数をロードしておきます。Scilabの場合、関数を定義してあるスクリプトファイル(.sce)をexecします。以下はHOME配下のscilabというフォルダ内にスクリプトを配置しているケースです。
exec('scilab\genSin.sce');
exec('scilab\plotFFT.sce');
サンプリング周波数Fsは10kHz、サンプル数4096点で、正弦波2つを重ね合わせた波形を入力信号としてみます。周波数1(freq1)は500Hz、周波数2(freq2)は2000Hzです。倍数にならない半端な値の方が良かったかと後で思いましたが、後の祭りというやつ。
Fs=10000; nSample=4096; phdeg=0; mag=1.0; freq1=500; [t, x1] = genSin(Fs, nSample, freq1, phdeg, mag); freq2=2000; [t, x2] = genSin(Fs, nSample, freq2, phdeg, mag); x = x1 + x2;
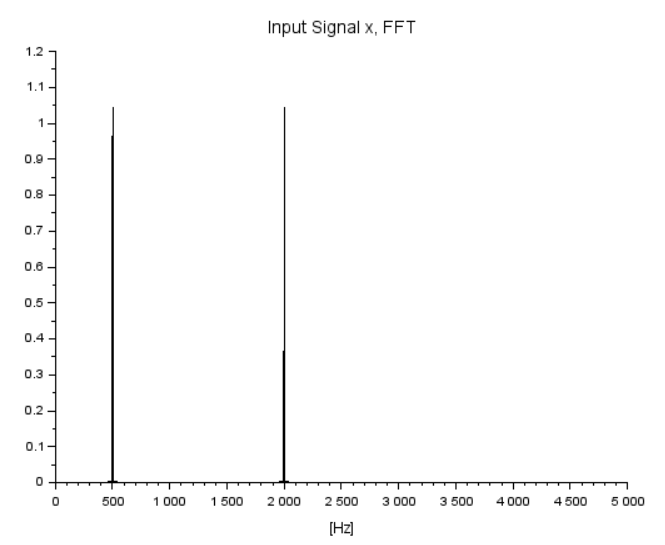
生成した入力信号 x を周波数プロット(FFT)してみます。
plotFFT(Fs, x, 1)
xtitle('Input Signal x, FFT');
500Hzと2000Hzにピークが現れておりますな。
念のため x の時間波形もプロットしておきます。
clf() plot2d3(x);
波形(一部拡大)はこんな感じ。2つの周波数か重なっているので結構ガタガタだな。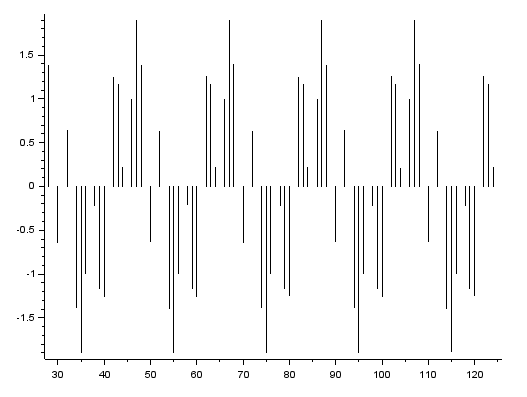
差分方程式を処理して出力信号 y を得る
元の差分方程式が簡単なので処理も簡単。こんな感じでやってみました。
y = zeros(1, nSample); a1=0.6; b0=1.0-a1; y(1,1) = b0 * x(1,1); for n = 2:nSample y(1,n) = a1 * y(1, n-1) + b0 * x(1, n); end;
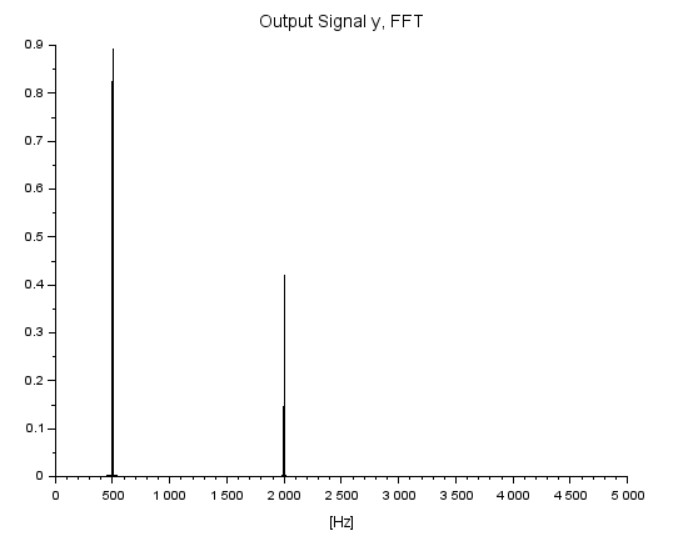
処理した結果の出力信号 y を周波数プロット(FFT)してみます。
plotFFT(Fs, y, 1)
xtitle('Output Signal y, FFT');
プロットはこんな感じ。500Hzと2000Hzにピークがあるのは変わらないけれども大分山の高さが低くなってないかい。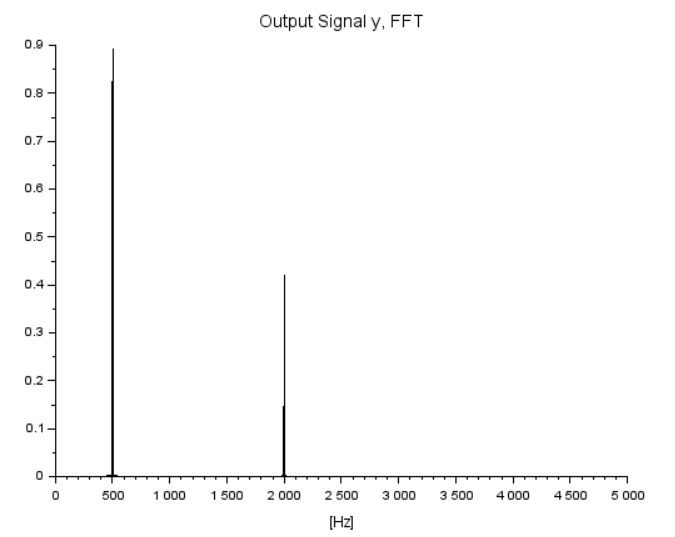
三上先生の教科書には、出力振幅Awの計算式が書かれていたので、ちとカンニングして、周波数1と周波数2でのAwを計算してみました。
微妙に大きいけれども、雰囲気は出ている? なぜ微妙に大きいのか突っ込まんかい、自分。。。
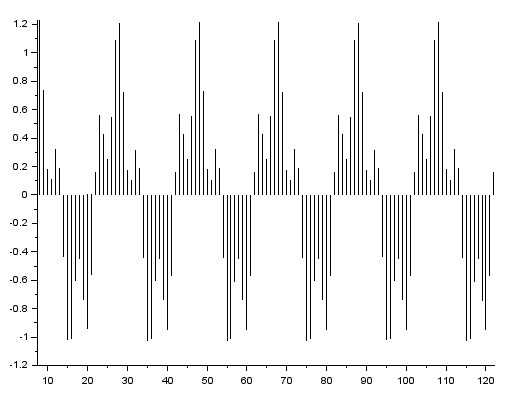
ツッコミをスルーして、y の時間波形のプロット。
clf() plot2d3(y);
波形(一部拡大)はこんな感じ。500Hzが目立ってきた?
まあ、そのとおりに計算すればその通りの結果が出そうな気がしてきた。大丈夫か?