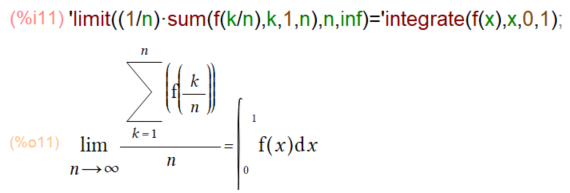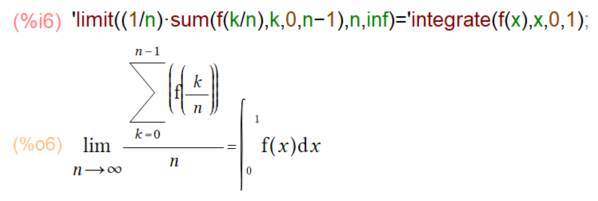このところ定積分を練習していた筈、トートツに級数の和が登場した感あり。しかし深い慮りがあると見ましたぜ。これから面積とか体積とか積分していくみたいなのですが、その礎として「n分割のnを無限にして足し合わせたならば」ということを置いておかないと気持ち悪りーと。そんなのあたり前じゃん、みたいに踏みつぶしたりしないのですな。
※「忘却の微分方程式」投稿順 index はこちら
※数学のお勉強のための以下の教科書(参考書、問題集?)の例題をMaximaの練習に使わせていただいております。
遥かなるかな太古の時代、大学生のときにこういう御本が欲しかったデス。今回の件の詳しい説明が必要な方は上記をご購入くだされや。テヘ。
※以下のMaxima/wxMaximaバージョンで実習させていただいております。
-
- Maxima 5.46.0
- wxMaxima 22.04.0
とりあえずMaxima様にお召し上がりいただいたけれども
このところ異常積分(広義積分)などをMaxima様にお願いしておりましたが、ほとんど何の事前準備もなく、そのままお召し上がりいただけばお答えが出てました。今回もか、と期待して入力してみたら、冒頭のアイキャッチ画像のようでした。
入力した式がそのまま返ってきておりますやん。素のままではダメなのね。
「重要公式」
拝読させていただいております(練習しているのはMaxima様だけれども)教科書には重要公式として以下が挙げられております。
および
です。なんでこうなるかはネタバレになるので教科書ごらんください。よくよく見れば、関数fのある区間をn分割し、そのnを無限大に細かくしたら定積分という「ありがちな」関係を示して居るようにも見えまする。要は、左辺のlimitの形に「帰着」させれば定積分にできるってことよな。
さて例題
もういちど極限値を求める級数の和を掲げると以下です。とても自分で解ける気がいたしませぬ。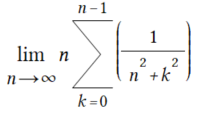
なお、Maxima様でのシグマ記号、sum()関数のマニュアルは以下の日本語ページに書かれてます。
さて、本題に戻ります。上のΣの中は下の式のシンボルA0です。このΣの中身の分母、分子をn2で割ってやって分子の方の 1/n2をΣの外に追い出してしまえばA1のように変形できます。まあ、公式は (k/n) で書かれているので、(k/n) が出てくるように変形できたということであります。A1を使って元の極限を書き直したものがA2です。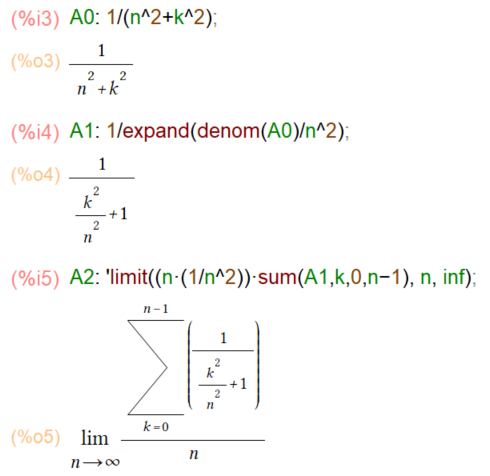
なんじゃらほい、公式の形になりましたぜ(教科書のご指導のたまものであります。)これでf(x)がどんな関数なのか明らかになりました。こうなればこっちのものだ(いや、Maxima様の)
なんだ、簡単な定積分じゃん、一撃よ(Maxima様にとっては。)
でもねえ、公式の形にもってくるところの変形、そして、公式を適用して定積分にするところ、Maxima様の上で処理できる関数みたいなものを定義したいものです。できるのか?それともそういうものがあるのか?